3.4.5. Поворот и параллельный перенос гиперболы
Вернёмся к демонстрационной гиперболе 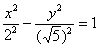 . Что произойдёт, если в
полученном уравнении поменять значения полуосей: . Что произойдёт, если в
полученном уравнении поменять значения полуосей: 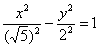 ? Для эллипса данный
трюк означал поворот на 90 градусов. Но здесь всё иначе! Уравнение ? Для эллипса данный
трюк означал поворот на 90 градусов. Но здесь всё иначе! Уравнение 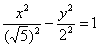 определяет совершенно другую гиперболу. Ну, хотя бы обратите внимание на иные вершины: определяет совершенно другую гиперболу. Ну, хотя бы обратите внимание на иные вершины: 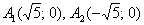 . .
Теперь рассмотрим уравнение 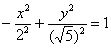 , которое, очевидно, тоже задаёт
гиперболу. Однако и оно не имеет отношения к исходному уравнению! Это предыдущая гипербола, повёрнутая на 90 градусов, с вершинами , которое, очевидно, тоже задаёт
гиперболу. Однако и оно не имеет отношения к исходному уравнению! Это предыдущая гипербола, повёрнутая на 90 градусов, с вершинами 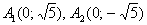 на оси ординат. на оси ординат.
И, наконец, оставшийся четвёртый случай 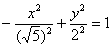 задаёт нашу гиперболу задаёт нашу гиперболу 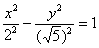 , повёрнутую на 90 градусов. Как быть, если в практической задаче встретилась
такая неканоническая запись? , повёрнутую на 90 градусов. Как быть, если в практической задаче встретилась
такая неканоническая запись?
Если требуется только построить кривую, то строим её именно в таком, неканоническом виде. Это довольно просто. Уравнения
асимптот гиперболы 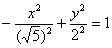 обладают обратными угловыми
коэффициентами: обладают обратными угловыми
коэффициентами: 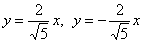 . .
Поскольку оси «поменялись ролями», то вершины будут расположены на оси ординат в точках 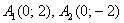 . Выразим верхнюю ветвь гиперболы: . Выразим верхнюю ветвь гиперболы:
 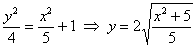
и найдём несколько дополнительных точек:
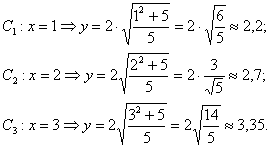 Отметим на чертеже найденные точки, симметричные им точки и аккуратно
соединим их линиями. Отметим на чертеже найденные точки, симметричные им точки и аккуратно
соединим их линиями.
Помимо геометрии, похожие графики требуется строить в некоторых задачах математического анализа.
Это то, что касаемо построения. Если же по условию требуется найти фокусы, эксцентриситет и т.д., то уравнение 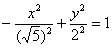 лучше привести к каноническому виду. Напоминаю, что это можно сделать двумя способами. Способ первый,
«чайниковский»: повернём гиперболу на лучше привести к каноническому виду. Напоминаю, что это можно сделать двумя способами. Способ первый,
«чайниковский»: повернём гиперболу на 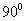 и запишем
уравнение в каноническом виде: и запишем
уравнение в каноническом виде: 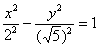 . Способ второй,
строгий: перейдём к системе координат . Способ второй,
строгий: перейдём к системе координат 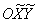 , которая получена поворотом
системы , которая получена поворотом
системы 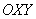 на на 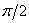 радиан против часовой стрелки, и запишем уравнение гиперболы в новой системе: радиан против часовой стрелки, и запишем уравнение гиперболы в новой системе: 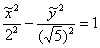
Параллельный перенос гиперболы доставляет заметно больше хлопот, чем таковой у эллипса. Но уравнение
похоже: 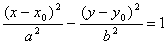 – оно задаёт гиперболу с действительной полуосью «а», мнимой
полуосью «бэ» и центром в точке – оно задаёт гиперболу с действительной полуосью «а», мнимой
полуосью «бэ» и центром в точке 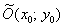 . .
Так, гипербола 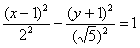 имеет центр симметрии в точке имеет центр симметрии в точке 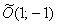 . Асимптоты, само собой, переместились вместе с гиперболой, их уравнения отыскиваются по формулам: . Асимптоты, само собой, переместились вместе с гиперболой, их уравнения отыскиваются по формулам: 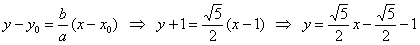 , ,
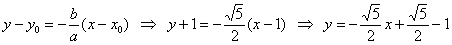 . .
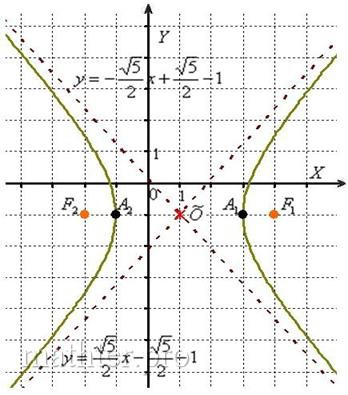 Полуоси Полуоси 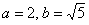 и расстояние от фокусов до центра симметрии и расстояние от фокусов до центра симметрии 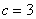 остались прежними, а вот координаты фокусов изменились с учётом параллельного переноса: остались прежними, а вот координаты фокусов изменились с учётом параллельного переноса:
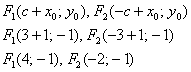
Если уравнение 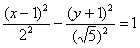 нужно привести к каноническому виду, то способы
аналогичны: нужно привести к каноническому виду, то способы
аналогичны:
по «чайниковски»: осуществим параллельный перенос гиперболы в начало координат и запишем её уравнение в виде 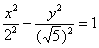 ; ;
и по строгости: осуществим параллельный перенос системы координат 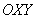 в точку в точку 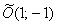 и запишем уравнение
гиперболы в системе и запишем уравнение
гиперболы в системе 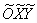 : : 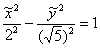 . .
 3.5.1. Парабола 3.5.1. Парабола
 3.4.4. Равносторонняя гипербола 3.4.4. Равносторонняя гипербола
| Оглавление |
|

 Аналитическая геометрия для «чайников»
Аналитическая геометрия для «чайников»
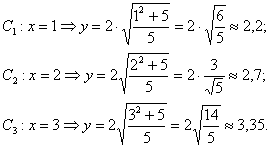 Отметим на чертеже найденные точки, симметричные им точки и аккуратно
соединим их линиями.
Отметим на чертеже найденные точки, симметричные им точки и аккуратно
соединим их линиями. Полуоси
Полуоси 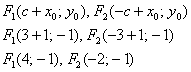
 3.5.1. Парабола
3.5.1. Парабола 3.4.4. Равносторонняя гипербола
3.4.4. Равносторонняя гипербола