|
Ваш репетитор, справочник и друг!
|
3.4.4. Равносторонняя гиперболаНа практике часто встречается гипербола с равными полуосями, такую гиперболу называют равносторонней. Если Прямые Так как Предлагаю закрепить теорию и практические навыки миниатюрной задачей: Задача 100 Построить гиперболу И я поздравляю вас с юбилейной задачей! Решение и чертёж в конце книги. Начнём тревожить беззаботное существование нашей кривой:
|
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Аналитическая геометрия для «чайников»
Аналитическая геометрия для «чайников»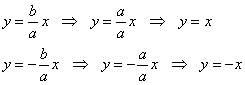
 3.4.5. Поворот и параллельный перенос гиперболы
3.4.5. Поворот и параллельный перенос гиперболы 3.4.3. Фокусы и эксцентриситет гиперболы
3.4.3. Фокусы и эксцентриситет гиперболы