|
Ваш репетитор, справочник и друг!
|
2.7. Системы линейных неравенствСистема линейных неравенств – это система, составленная из линейных неравенств. …Обожаю такие определения :) Что значит решить систему линейных неравенств? Ответ на этот вопрос зависит от количества переменных. У нас их две. Решить систему линейных неравенств с двумя переменными – это значит найти множество точек плоскости, которые удовлетворяют каждому неравенству системы. В качестве простейших примеров рассмотрим системы неравенств, определяющих координатные четверти прямоугольной
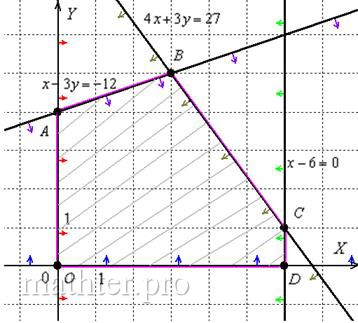
системы координат. Вспоминаем «рисунок двоечников», уменьшу его в размерах: Аналогично: Система линейных неравенств может не иметь решений, то есть, быть несовместной. Снова простейший пример: Решением системы неравенств может быть прямая, например: Но самый распространённый случай, это когда решением системы является некоторая область плоскости. Область решений может быть не ограниченной (например, координатные четверти) либо ограниченной. Ограниченная область решений называется многоугольником решений системы, и это самый популярный вариант: Задача 92 Решить систему линейных неравенств Сколько может быть неравенств в системе? Да сколько угодно. Решение: и то, что неравенств многовато, пугать не должно, главное придерживаться рационального алгоритма построения области решений: 1) Сначала разбираемся с простейшими неравенствами. Неравенства 3) На последнем шаге решаем неравенства «с полным боекомплектом»: Ответ: многоугольник с вершинами Аналогичная задача для самостоятельного решения: Задача 93 Решить систему и найти координаты вершин полученной области А вот здесь для нахождения некоторых вершин уже придётся решать системы, поскольку координаты точек не очевидны. И это, кстати, хороший способ проверить правильность чертежа. У вас, скорее всего, будут другие буквенные обозначения, но это не принципиально, главное, правильно определить и построить область. Не удивляйтесь, что все неравенства нестрогие – именно они часто используются в прикладных задачах, например, в задачах линейного программирования.
|
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Аналитическая геометрия для «чайников»
Аналитическая геометрия для «чайников» Система неравенств
Система неравенств 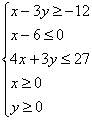
 2) Второе по простоте неравенство
2) Второе по простоте неравенство 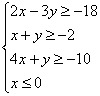
 2.8. Как научиться решать задачи по геометрии?
2.8. Как научиться решать задачи по геометрии? 2.6. Линейные неравенства
2.6. Линейные неравенства