|
Ваш репетитор, справочник и друг!
|
2.6. Линейные неравенстваУравнение хорошо, а неравенство – не хуже. Различают два типа линейных неравенств: 1) Строгие неравенства: 2) Нестрогие неравенства: Какой геометрический смысл этих неравенств? Если линейное уравнение Начнём с простейших линейных неравенств. Голубая мечта любого двоечника – координатная плоскость, на которой нет ничегошеньки. Даже стрелочки для
вас забыл:)) Рассмотрим неравенство В том случае, если неравенство нестрогое Аналогично, неравенству С осью ординат – неравенство На втором шаге рассмотрим неравенства, в которых отсутствует одна из переменных, «игрек»: С такими неравенствами можно разобраться двумя способами, и мы разберём оба подхода. Попутно вспомним «школьные» действия с неравенствами, которые во многом напоминают действия с уравнениями: Задача 86 Решить линейные неравенства:
Что значит решить линейное неравенство? Решить линейное неравенство – это значит найти полуплоскость, точки которой удовлетворяют данному неравенству (+ саму прямую, если неравенство нестрогое). Решение, как правило, графическое, удобнее сразу выполнить чертёж, а потом всё закомментировать: Способ первый весьма напоминает историю с координатными осями, которую мы рассмотрели выше. Идея состоит в преобразовании
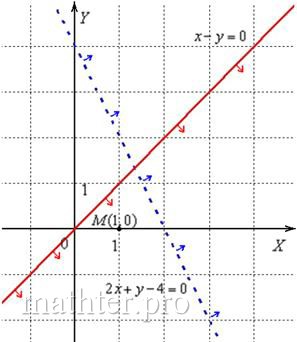
неравенства – чтобы в левой части оставить одну переменную без всяких констант, в данном случае – переменную «икс». Каков смысл неравенства Сама прямая проведена пунктиром по той причине, что неравенство строгое, и точки, принадлежащие прямой Способ второй, универсальный. ЧИТАЕМ ОЧЕНЬ ВНИМАТЕЛЬНО! Сначала чертим прямую Теперь выбираем любую точку плоскости, не принадлежащую прямой. В большинстве случаев самая лакомая точка, конечно Получено неверное неравенство (простыми словами, неправда), значит, точка Ключевое правило: – Если какая-либо точка, не принадлежащая прямой, не удовлетворяет неравенству, то и ВСЕ точки этой полуплоскости не удовлетворяют данному неравенству. – Если какая-либо точка, не принадлежащая прямой, удовлетворяет неравенству, то и ВСЕ точки этой полуплоскости удовлетворяют данному неравенству Можете протестировать: любая точка справа от прямой Деваться некуда, неравенству б) Решим неравенство Способ первый. Преобразуем неравенство, чтобы получить слева «игрек»:
Если обе части неравенства умножить на отрицательное число, то знак неравенства меняется на противоположный (например, если
было Умножим обе части неравенства на Начертим прямую Проанализировав полученное неравенство Нужная полуплоскость штрихуется либо помечается стрелочками. Способ второй. Начертим прямую Получено верное неравенство, значит, точка Решение задачи обозначено красными стрелочками на чертеже выше. Лично мне нравится больше первый способ решения, хотя второй, на мой взгляд, чуть проще. Задача 87 Решить линейные неравенства: Постарайтесь решить задачу двумя способами (к слову, это хороший способ проверки решения). Чертёж с графическим решением в конце книги. Думаю, после всех проделанных в примерах действий вам Переходим к рассмотрению третьего, общего случая, когда в неравенстве присутствуют обе переменные: Во всех перечисленных случаях используется универсальный метод решения с подстановкой точки: Задача 88 Найти полуплоскости, соответствующие следующим неравенствам: Решение: Выбираем подопытную точку плоскости, которая не принадлежит данной прямой, например, Получено неверное неравенство, значит, точка Таким образом, решением неравенства Выберем произвольную точку, не принадлежащую прямой Получено верное неравенство, значит, точка Задача 89 Найти полуплоскости, соответствующие неравенствам: Тренируемся! – примерный образец чистового оформления решения в конце книги. Разберём обратную задачу: Задача 90 а) Дана прямая б) Дана прямая Здесь нет надобности в чертеже и решение чисто аналитическое: а) Составим вспомогательный многочлен б) Составим многочлен Ответ: Творческая задача для самостоятельного решения: Задача 91 Среди точек Аналитическое решение и ответ в конце книги.
|
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Аналитическая геометрия для «чайников»
Аналитическая геометрия для «чайников» Как известно, ось абсцисс
Как известно, ось абсцисс 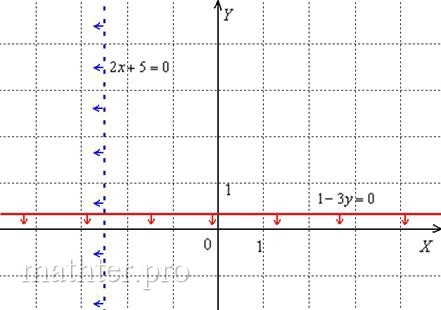
 б) Решим неравенство
б) Решим неравенство  2.7. Системы линейных неравенств
2.7. Системы линейных неравенств 2.5.8. Как найти проекцию вектора на прямую?
2.5.8. Как найти проекцию вектора на прямую?