|
Ваш репетитор, справочник и друг!
|
2.8. Как научиться решать задачи по геометрии?Откуда такой вопрос? Дело в том, что задач по геометрии можно придумать очень много, и никакой учебник не вместит в себя всё множество и
разнообразие примеров. Увы, это не производная с 5 правилами и
жесткими алгоритмами решения. ЧТО НУЖНО знать и уметь для успешного решения задач по ангему? Ступень первая. Требуется освоить азы аналитической геометрии. Векторы (!), информацию о прямой на плоскости, простейшие задачи с прямой и другие темы, которые мы изучим позже. Образно говоря, это кирпичики фундамента, на котором строится всё остальное. Без него никак. Уровень второй, когда вы уже обладаете элементарными знаниями и навыками решения простейших задач. Но вот бывает же так, читаешь условие задачи, и… не понятно, что делать, не понятно, как подступиться к решению…. Что делать? Не бояться задачи, которая вам не понятна! Во-первых, следует установить – это «плоская» или пространственная задача? Тупо посмотреть, сколько координат у векторов и точек, две или три? Результаты первого шага уже неплохи, ведь удалось отсечь громадное количество ненужной информации! Второе. Условие, как правило, озаботит вас некоторой геометрической фигурой, Третье. ВСЕГДА старайтесь выполнять чертёж (на черновике / чистовике / мысленно / в сердце), даже если этого не требуется по условию. В «плоских» задачах сам Евклид велел взять в руки линейку с карандашом – и не только для того, чтобы понять условие, но и в целях самопроверки. При этом наиболее удобный масштаб 1 единица = 1 см (2 тетрадные клетки). Для пространственных заданий выполняем схематический рисунок, который тоже поможет проанализировать условие. Чертёж или схематический чертёж зачастую сразу позволяет увидеть путь решения задачи. Но, конечно, для этого нужно знать фундамент и рубить в свойствах геометрических фигур (см. предыдущие пункты) Четвёртое. Разработка алгоритма решения. Многие задачи являются многоходовыми, и поэтому решение и его оформление очень удобно разбивать на пункты. Нередко алгоритм сразу же приходит в голову, после того как вы прочитали условие или выполнили чертёж. В случае возникновения трудностей начинаем с ВОПРОСА задачи. Например, по условию требуется построить прямую. И здесь самый логичный вопрос такой: А что нужно знать, чтобы построить эту прямую? Предположим, точка нам известна, тогда нужно узнать ещё одну точку или направляющий вектор. Задаём следующий вопрос: Как найти эту точку / направляющий вектор? Откуда? и т.д. Кстати, этот пункт полезен не только в геометрии и не только в математике. И не только в науках,… впрочем, не будем развивать попсовые темы, сейчас геометрия! Иногда случается «затык» – не решается задача и всё тут. Причины «стопора» могут быть следующими: – Серьёзный пробел в элементарных знаниях. Иными словами, вы не знаете или (и) не видите какой-то очень простой вещи. Да просто неправильно извлекаете корень или упрощаете трёхэтажную дробь (см. Приложение Школьные Материалы). – Незнание свойств геометрических фигур. Следует отметить, что некоторые из них имеют специфические и малоизвестные свойства, и поэтому я рекомендую не ограничиваться упомянутым выше Приложением, а посмотреть более подробные источники, хотя бы Википедию, где авторы стараются упомянуть всё-всё-всё. – Задача попалась трудная. Да, так бывает. И тут нет смысла париться часами, обратитесь за консультацией к преподавателю, сокурсникам или задайте вопрос на форуме. Причём, его постановку лучше сделать конкретной – о том участке решения, который вам не понятен. Клич в виде «Как решить задачу?» выглядит не очень-то…. Этап пятый. Решаем-проверяем, решаем-проверяем, решаем-проверяем-даём ответ. Каждый пункт задачи выгодно проверять СРАЗУ после его выполнения. Это поможет немедленно обнаружить ошибку. Естественно, никто не запрещает быстренько прорешать задачу целиком, но это чревато переписыванием всего решения заново (порой, несколько страниц). Шестое: решаем, решаем, решаем! А теперь самый главный, Седьмой секрет: Получаем удовольствие! И начнём мы прямо сейчас. Пройдёмся по нити алгоритма, который я только что рассмотрел в своём маленьком научном труде. Задач будет две, но мало не покажется =) Задача 94 Даны три вершины Шаг первый: очевидно, что речь идёт о «плоской» задаче. Шаг второй: в задаче речь идёт о параллелограмме. Все помнят такую фигуру? ;) Шаг третий: Выполним чертёж, на котором отметим три известные вершины, да и вообще всё остальное, искомую точку Шаг четвёртый: Разработка алгоритма решения. Первое, что приходит в голову – точку Шаг5 Прорешиваем самостоятельно и проверяем каждый пункт: 1) Противоположные стороны 2) Составим уравнение прямой 3) Противоположные стороны 4) Составим уравнение 5) Теперь уравнения прямых Записываем ответ: ... – не забываем об этом важном элементе решения! Задача довольно-таки простая, но существует ещё более короткий путь! Второй способ решения: диагонали параллелограмма своей точкой пересечения делятся пополам (точку 1) С помощью формул координат середины отрезка найдём точку 2) Рассмотрим диагональ Знание свойств параллелограмма позволило значительно сократить решение! Как говорится, знание – сила, а незнание – рабочая сила. Переходим к очень популярной задаче, которая встречается практически в каждом сборнике, в каждой методичке:
|
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Аналитическая геометрия для «чайников»
Аналитическая геометрия для «чайников»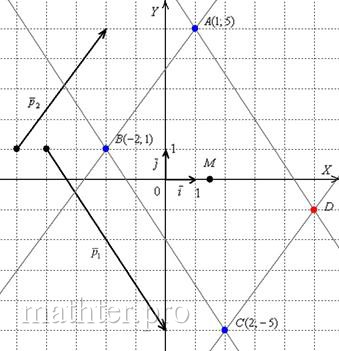 Построить – это хорошо, но решение нужно оформить
аналитически.
Построить – это хорошо, но решение нужно оформить
аналитически. 2.9. Типовая задача с треугольником
2.9. Типовая задача с треугольником 2.7. Системы линейных неравенств
2.7. Системы линейных неравенств