2.2.2. Как составить уравнение прямой
по точке и направляющему вектору?
Что делать, когда одна из координат 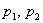 равна нулю, мы разберёмся в практических примерах ниже. Кстати, заметьте – сразу обе координаты равняться нулю не могут, так как нулевой вектор не задаёт конкретного направления. равна нулю, мы разберёмся в практических примерах ниже. Кстати, заметьте – сразу обе координаты равняться нулю не могут, так как нулевой вектор не задаёт конкретного направления.
Задача 61
Составить уравнение прямой по точке 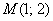 и направляющему вектору и направляющему вектору 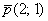 . .
Решение: Используем формулу 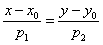 . В данном случае: . В данном случае:
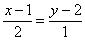
С помощью свойств пропорции* (Школьные материалы) избавляемся от дробей:
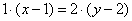 (* технически здесь также можно умножить обе части на 2) (* технически здесь также можно умножить обе части на 2)
и приводим уравнение к общему виду:
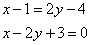
Ответ: 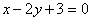
Чертежа в таких примерах делать не нужно, но понимания ради:
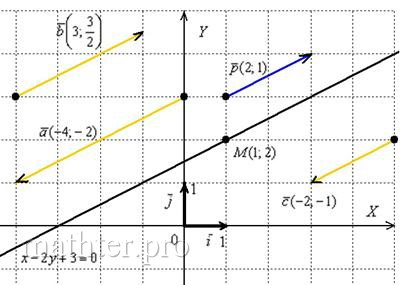
На чертеже мы видим исходную точку 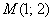 , исходный направляющий вектор , исходный направляющий вектор 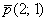 (его можно отложить от любой точки плоскости) и построенную прямую (его можно отложить от любой точки плоскости) и построенную прямую 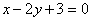 . .
Как отмечалось в начале параграфа, у прямой бесконечно много направляющих векторов, и все они коллинеарны. Для примера я нарисовал три таких вектора: 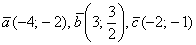 . Какой бы направляющий вектор мы ни выбрали, в результате всегда получится одно и то же уравнение прямой . Какой бы направляющий вектор мы ни выбрали, в результате всегда получится одно и то же уравнение прямой 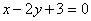 . .
Составим уравнение прямой по точке 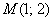 и, например, направляющему вектору и, например, направляющему вектору 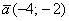 : :
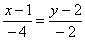
разруливаем пропорцию:
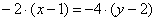
Делим обе части на –2 и получаем знакомое уравнение:
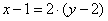
Желающие могут аналогичным образом протестировать векторы 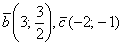 или любой другой коллинеарный вектор. или любой другой коллинеарный вектор.
Теперь решим обратную задачу:
 2.2.3. Как найти направляющий вектор по общему уравнению прямой? 2.2.3. Как найти направляющий вектор по общему уравнению прямой?
 2.2.1. Общее уравнение и направляющий вектор прямой 2.2.1. Общее уравнение и направляющий вектор прямой
| Оглавление |
|