|
Ваш репетитор, справочник и друг!
|
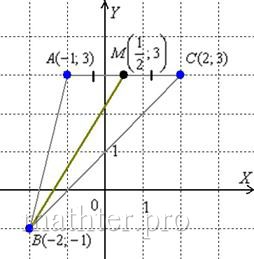
2.9. Типовая задача с треугольникомМногие помнят из школы признаки равенства треугольников, признаки подобия треугольников и мучительное заучивание доказательств теорем. Как в сердцАх сказал один мой одноклассник, «не понимаю, на### доказывать равенство треугольников, если и так видно, что они одинаковые». Мы тоже не будем ничего доказывать, поскольку аналитическая геометрия рассматривает треугольник совсем с другой стороны. Типовая задача, как правило, формулируется так: Даны три вершины треугольника. Требуется найти… много чего требуется найти…. Повезёт, если будет пункта 3-4, но чаще всего их 5-6 и даже больше. И вам повезло – разберём всё! Или почти всё: Задача 95 Даны вершины треугольника 1) составить уравнения сторон С чего начать решение? Начать целесообразно с выполнения чертежа. По условию этого можно не делать, но для самоконтроля и
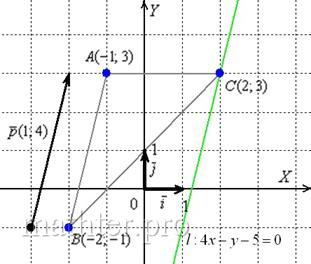
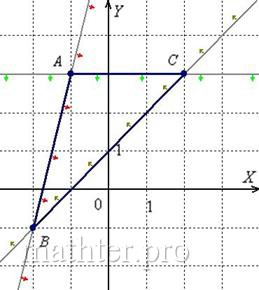
самопроверки всегда строим чертёж на черновике, не устану это рекомендовать: Ещё раз напоминаю, что самый выгодный масштаб 1 единица = 1 см (2 тетрадные клетки). Всё хорошо видно, и расстояния удобно измерять линейкой. Вперёд без страха и сомнений: 1) Составим уравнения сторон Составим уравнение стороны Для проверки мысленно либо на черновике подставляем координаты каждой точки в полученное уравнение. Теперь
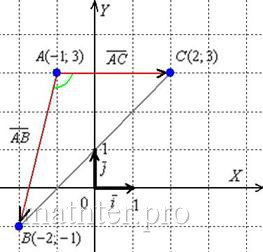
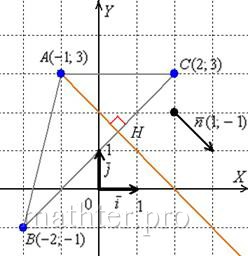
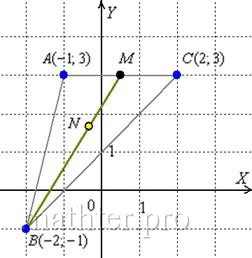
найдём угловой коэффициент. Для этого перепишем общее уравнение в виде уравнения с угловым коэффициентом: Таким образом, угловой коэффициент: Самостоятельно разбираемся со сторонами 2) Найдём длину стороны Сторону легко измерить обычной линейкой, хотя это не сильно строгая проверка :) 3) Найдём Используем формулу Таким образом: Внимание! При выполнении этого пункта лучше не использовать формулы ориентированного угла между прямыми, так как они всегда дают острый угол. 4) Составим уравнение прямой Из общего уравнения прямой 5) Составим уравнение высоты Из уравнения стороны Обратите внимание, что координаты точки Иногда уравнение высоты находят из соотношения угловых коэффициентов перпендикулярных прямых: Длину высоты можно найти двумя способами. Существует окольный путь: а) находим б) находим длину отрезка Но зачем? – ведь есть удобная формула расстояния от точки 6) Вычислим площадь треугольника. Используем «школьную» формулу: 7) Уравнение медианы а) Найдём точку б) Уравнение медианы
8) Найдём точку пересечения
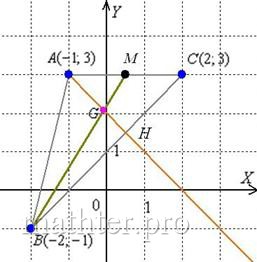
Первое уравнение умножили на 5, складываем их почленно: 9) Биссектриса делит угол пополам: Из свойств биссектрисы внутреннего угла следует соотношение длин следующих отрезков: Длины сторон уже найдены в предыдущих пунктах: Таким образом, Примечание: на последнем шаге я умножил числитель и знаменатель на сопряжённое выражение Разбираемся со второй координатой: аким образом: И предчувствие вас не обмануло, уравнение биссектрисы Проверил, всё сходится. На практике, конечно, вычисления почти всегда будут проще. Никого не хотел запугать, так уж получилось =) 10) Найдём центр тяжести треугольника. Но сначала поймём, что такое центр тяжести плоской фигуры. Мысленно вырежьте из тонкого однородного картона любую фигуру. …Почему-то фигура зайца в голову пришла. Так вот: если слегка насадить данную фигуру центром тяжести (какой же я изверг =)) на вертикально расположенную иголку, то теоретически фигура не должна свалиться. Центром тяжести треугольника является точка пересечения его медиан. В треугольнике три медианы и пересекаются они в одной точке.
Из пункта 7 нам уже известна одна из медиан: Напрашивается очевидный алгоритм: можно найти уравнение второй медианы (любой из двух оставшихся) и точку пересечения этих медиан. Но есть путь
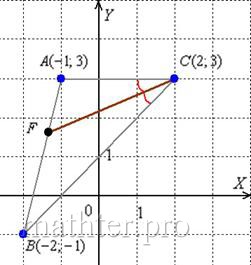
короче! Нужно только знать полезное свойство: Точка пересечения медиан делит каждую из медиан в
отношении Таким образом, центр тяжести треугольника: 11) Составим систему линейных неравенств, определяющих треугольник. Для удобства я перепишу найденные уравнения сторон: Рассмотрим прямую Внимание! Если вам не понятен этот алгоритм, то обратитесь к Задаче 90. Рассмотрим прямую И, наконец, для Итак, треугольник Готово. Какой можно сделать вывод?
Многие задачи аналитической геометрии прозрачны и просты, Следует отметить, что по настоящему трудные задачи в аналитической геометрии встречаются редко, и вы справитесь практически с любой из них! Главное, придерживаться методики решения и проявить маломальское упорство. Ну что, может ещё задачку? Да ладно, не надо стесняться, я же по глазам вижу, что хотите =) Но сейчас на очереди другая увлекательная тема, продолжаем изучать геометрию плоскости:
|
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Аналитическая геометрия для «чайников»
Аналитическая геометрия для «чайников»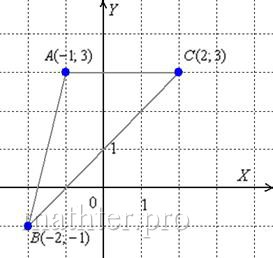
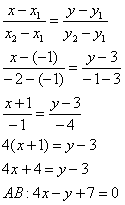
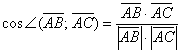 .
.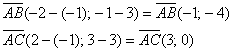
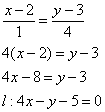
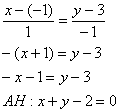
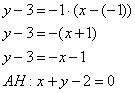
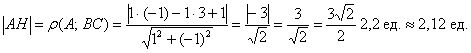
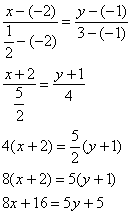
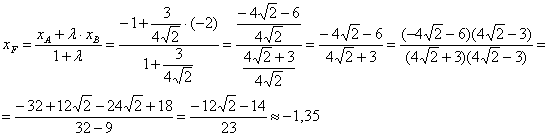
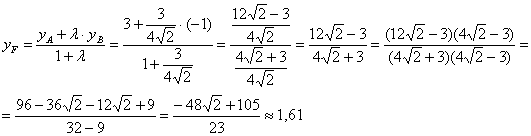
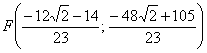
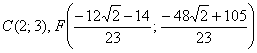 по формуле
по формуле 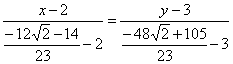
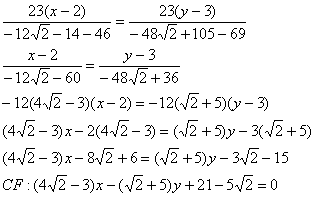
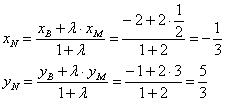
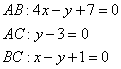
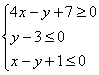
 3.1. Алгебраическая линия и её порядок
3.1. Алгебраическая линия и её порядок 2.8. Как научиться решать задачи по геометрии?
2.8. Как научиться решать задачи по геометрии?