2.5.7. Как найти угол между прямыми?
Новая картинка за очередным поворотом:
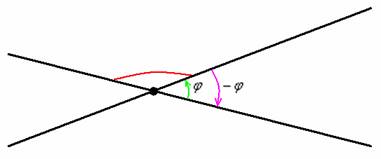 В геометрии за угол между двумя прямыми принимается
МЕНЬШИЙ угол, из чего автоматически следует, что он не может быть тупым. На рисунке угол, обозначенный красной дугой, не считается углом
между пересекающимися прямыми. А считается таковым его «зелёный» сосед В геометрии за угол между двумя прямыми принимается
МЕНЬШИЙ угол, из чего автоматически следует, что он не может быть тупым. На рисунке угол, обозначенный красной дугой, не считается углом
между пересекающимися прямыми. А считается таковым его «зелёный» сосед 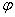 или
отрицательно ориентированный «малиновый» угол или
отрицательно ориентированный «малиновый» угол 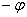 . Если прямые
перпендикулярны, то за угол между ними можно принять любой из 4 углов. . Если прямые
перпендикулярны, то за угол между ними можно принять любой из 4 углов.
…что-то не понятно? Срочно изучаем Приложение Тригонометрия!
Однако ещё раз: чем отличаются углы 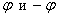 ? Ориентацией (направлением «прокрутки» угла).
Напоминаю, что отрицательно ориентированный угол «прокручивается» по часовой стрелке и записывается со знаком «минус».
Следует отметить, что ориентацию угла часто не принимают во внимание, и рассматривают «просто угол», который ? Ориентацией (направлением «прокрутки» угла).
Напоминаю, что отрицательно ориентированный угол «прокручивается» по часовой стрелке и записывается со знаком «минус».
Следует отметить, что ориентацию угла часто не принимают во внимание, и рассматривают «просто угол», который 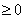 . .
Как найти угол между двумя прямыми? Существуют три основные формулы.
Способ первый. Рассмотрим две прямые, заданные общими уравнениями в декартовой системе
координат: 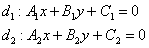
Если 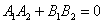 , то прямые перпендикулярны ( , то прямые перпендикулярны (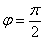 либо либо 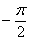 ). ).
Если 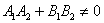 , то прямые не перпендикулярны и ориентированный угол , то прямые не перпендикулярны и ориентированный угол 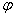 между ними можно вычислить с помощью
формулы: между ними можно вычислить с помощью
формулы:
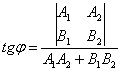
Знаменатель этой формулы – в точности, скалярное произведение направляющих векторов: 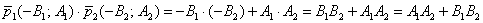 ,
которое равно нулю тогда и только тогда, когда векторы ортогональны. …надеюсь, не забыли. ,
которое равно нулю тогда и только тогда, когда векторы ортогональны. …надеюсь, не забыли.
Задача 83
Найти угол между прямыми 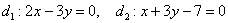 , заданными в декартовой системе координат. , заданными в декартовой системе координат.
Исходя из вышесказанного, решение удобно оформить в два шага:
1) Вычислим произведение:
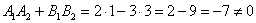 , значит, прямые не перпендикулярны. , значит, прямые не перпендикулярны.
2) Угол между прямыми найдём с помощью формулы:
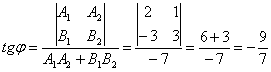
И с помощью обратной функции (см. Приложение Тригонометрия) легко найти сам угол, при этом используем нечётность арктангенса:
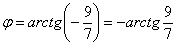
Ответ: 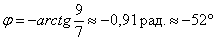
В ответе указываем точное значение, а также приближённое значение (желательно и в градусах, и в радианах), вычисленное с помощью
калькулятора.
Ну, минус, так минус, ничего страшного, вот геометрическая иллюстрация:
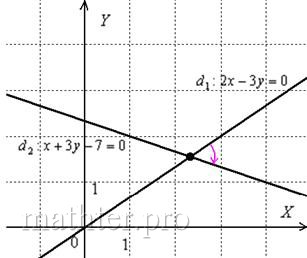
Неудивительно, что угол получился отрицательной ориентации, ведь в условии задачи «первым номером» идёт прямая 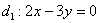 и «открутка» угла началась именно с неё. Если очень хочется получить положительное значение, то нужно
поменять прямые местами, то есть коэффициенты и «открутка» угла началась именно с неё. Если очень хочется получить положительное значение, то нужно
поменять прямые местами, то есть коэффициенты 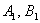 взять из второго уравнения взять из второго уравнения 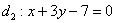 , а коэффициенты , а коэффициенты 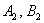 – из первого уравнения – из первого уравнения 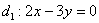 . Короче
говоря, начать нужно . Короче
говоря, начать нужно
с прямой 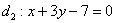 . .
Скрывать не буду, сам подбираю прямые в том порядке, чтобы угол получился положительным. Так красивее, но не более того.
Способ второй, он удобен, когда прямые заданы уравнениями с
угловым коэффициентом: 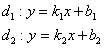 (в декартовых координатах). (в декартовых координатах).
Если 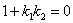 , то прямые перпендикулярны ( , то прямые перпендикулярны (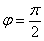 либо либо 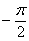 ). ).
Если 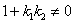 , то ориентированный угол , то ориентированный угол 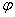 между ними можно найти с помощью формулы: между ними можно найти с помощью формулы:
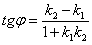 , и на самом деле это частный случай предыдущей формулы. , и на самом деле это частный случай предыдущей формулы.
К слову, из равенства 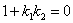 следует полезная взаимосвязь угловых
коэффициентов перпендикулярных прямых: следует полезная взаимосвязь угловых
коэффициентов перпендикулярных прямых: 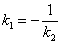 , которая используется в некоторых
задачах. , которая используется в некоторых
задачах.
Решим Задачу 83 вторым способом, для этого перепишем прямые в нужном виде:
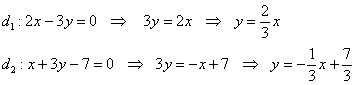
Таким образом, угловые коэффициенты: 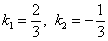 , и алгоритм похож: , и алгоритм похож:
1) Проверим, будут ли прямые перпендикулярны:
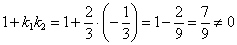 , значит, прямые не перпендикулярны. , значит, прямые не перпендикулярны.
2) Используем формулу:
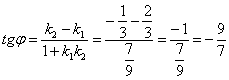
Ответ: 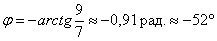
И третий способ состоит в нахождении угла между направляющими векторами прямых с помощью скалярного произведения: 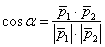 , но здесь не принимается во внимание ориентация угла (по любому получится , но здесь не принимается во внимание ориентация угла (по любому получится 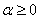 ). Кроме того, он может оказаться тупым, и тогда придётся делать оговорку, что угол между
прямыми – это меньший угол, и из ). Кроме того, он может оказаться тупым, и тогда придётся делать оговорку, что угол между
прямыми – это меньший угол, и из 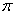 радиан (не из радиан (не из 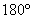 !) вычитать получившийся арккосинус. !) вычитать получившийся арккосинус.
Какой способ выбрать? Ориентируйтесь на вашу задачу, методичку или ситуацию.
Задача 84
Найти угол между прямыми 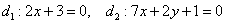 . .
Самостоятельно, всеми тремя способами! Решение и ответ в конце книги.
И по просьбам учащихся ещё один пункт:
 2.5.8. Как найти проекцию вектора на прямую? 2.5.8. Как найти проекцию вектора на прямую?
 2.5.6. Как найти расстояние между параллельными прямыми? 2.5.6. Как найти расстояние между параллельными прямыми?
| Оглавление |
|

 Аналитическая геометрия для «чайников»
Аналитическая геометрия для «чайников» В геометрии за угол между двумя прямыми принимается
МЕНЬШИЙ угол, из чего автоматически следует, что он не может быть тупым. На рисунке угол, обозначенный красной дугой, не считается углом
между пересекающимися прямыми. А считается таковым его «зелёный» сосед
В геометрии за угол между двумя прямыми принимается
МЕНЬШИЙ угол, из чего автоматически следует, что он не может быть тупым. На рисунке угол, обозначенный красной дугой, не считается углом
между пересекающимися прямыми. А считается таковым его «зелёный» сосед 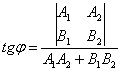
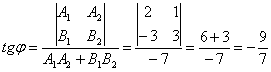

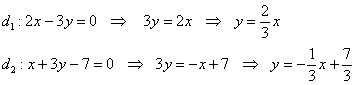
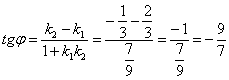
 2.5.8. Как найти проекцию вектора на прямую?
2.5.8. Как найти проекцию вектора на прямую?  2.5.6. Как найти расстояние между параллельными прямыми?
2.5.6. Как найти расстояние между параллельными прямыми?