2.5.4. Как найти прямую, перпендикулярную данной?
В отличие от предыдущих задач п. 2.5, рассмотренные ниже схемы работают лишь в декартовой системе
координат (но не в общем аффинном случае):
Задача 79
Прямая задана уравнением 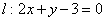 в декартовой системе координат. Составить
уравнение перпендикулярной прямой в декартовой системе координат. Составить
уравнение перпендикулярной прямой 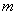 , проходящей через точку , проходящей через точку 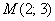 . .
Решение: по условию известна точка 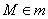 ( (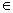 – значок принадлежности), и нам неплохо бы найти направляющий вектор прямой – значок принадлежности), и нам неплохо бы найти направляющий вектор прямой 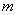 . Так как прямые перпендикулярны, то фокус прост: из уравнения . Так как прямые перпендикулярны, то фокус прост: из уравнения 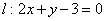 «снимаем» вектор нормали: «снимаем» вектор нормали: 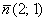 , который и будет направляющим вектором прямой , который и будет направляющим вектором прямой 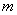 . .
Уравнение прямой 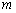 составим по точке составим по точке 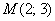 и направляющему вектору и направляющему вектору 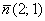 : :
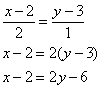
Ответ: 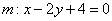
Развернём геометрический этюд:
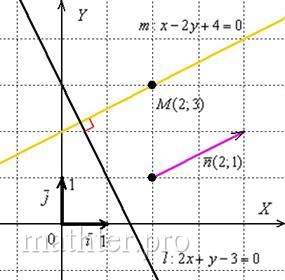 И аналитическая проверка решения: И аналитическая проверка решения:
1) Из уравнений 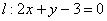 , , 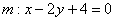 вытаскиваем направляющие векторы вытаскиваем направляющие векторы 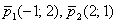 и с помощью скалярного произведения приходим к выводу, что прямые действительно
перпендикулярны: и с помощью скалярного произведения приходим к выводу, что прямые действительно
перпендикулярны:
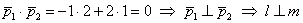 . .
Кстати, можно использовать векторы нормали, это даже проще.
2) Проверяем, удовлетворяет ли точка  полученному уравнению полученному уравнению 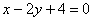
Оба пункта легко выполнить устно!
Самостоятельно:
Задача 80
Найти точку пересечения перпендикулярных прямых 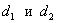 , если известно уравнение , если известно уравнение 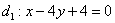 в декартовой системе координат и точка в декартовой системе координат и точка 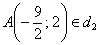 . .
В задаче несколько действий, поэтому решение удобно оформить по пунктам.
И наше увлекательное путешествие продолжается:
 2.5.5. Как вычислить расстояние от точки до прямой? 2.5.5. Как вычислить расстояние от точки до прямой?
 2.5.3. Как найти точку пересечения прямых? 2.5.3. Как найти точку пересечения прямых?
| Оглавление |
|

 Аналитическая геометрия для «чайников»
Аналитическая геометрия для «чайников»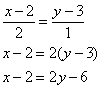
 И аналитическая проверка решения:
И аналитическая проверка решения: 2.5.5. Как вычислить расстояние от точки до прямой?
2.5.5. Как вычислить расстояние от точки до прямой? 2.5.3. Как найти точку пересечения прямых?
2.5.3. Как найти точку пересечения прямых?