|
Ваш репетитор, справочник и друг!
|
2.5.3. Как найти точку пересечения прямых?Если прямые Как найти точку пересечения прямых? Решить систему. И вот вам, кстати, геометрический смысл системы двух линейных уравнений с двумя неизвестными – это две пересекающиеся (чаще
всего) прямые. И реже: Задача 77 Найти точку пересечения прямых Существуют два способа решения – графический и аналитический. Графический способ состоит в том, чтобы просто начертить данные прямые и узнать точку пересечения непосредственно из чертежа: Для проверки следует подставить её координаты в уравнение каждой прямой, они должны подойти и там, и там. Графический способ, конечно, неплох, но существует и заметные минусы. Нет, дело не в том, что так решают семиклассники, дело в том, что на правильный и ТОЧНЫЙ чертёж уйдёт время. Кроме того, некоторые прямые построить не так-то просто, да и сама точка пересечения может находиться где-нибудь в тридесятом царстве за пределами тетрадного листа. Поэтому точку пересечения Проверка тривиальна – координаты точки пересечения должны удовлетворять каждому уравнению системы. К слову, этой задачей мы заодно рассмотрели графический способ решения системы двух линейных уравнений с двумя неизвестными. Задача 78 Найти точку пересечения прямых Это задача для самостоятельного решения, которое удобно разбить на несколько этапов. Анализ условия подсказывает, что нужно: 1) составить уравнение прямой Разработка алгоритма действий типична для геометрических задач, и я на этом буду неоднократно заострять внимание. В первой части параграфа мы узнали, как построить прямую, параллельную данной, и сейчас избушка на курьих ножках разворачивается на 90 градусов:
|
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Аналитическая геометрия для «чайников»
Аналитическая геометрия для «чайников»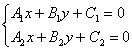
 Искомая точка:
Искомая точка: 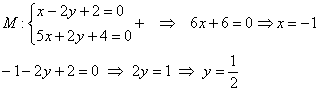
 2.5.4. Как найти прямую, перпендикулярную данной?
2.5.4. Как найти прямую, перпендикулярную данной? 2.5.2. Как найти прямую, параллельную данной?
2.5.2. Как найти прямую, параллельную данной?