Ваш репетитор, справочник и друг!

Аналитическая геометрия для «чайников»

2.5.1. Взаимное расположение двух прямых

Рассмотрим две прямые, уравнения которых заданы в общем виде:

Тот случай, когда зал подпевает хором. Две прямые могут:

1) совпадать;

2) быть параллельными: ;

3) или пересекаться в единственной точке: .

Справка: – это математический знак пересечения.

Как определить взаимное расположение двух прямых?

Начнём с первого случая:

1) Две прямые совпадают, тогда и только тогда, когда их соответствующие коэффициенты пропорциональны, то есть, существует такое число «лямбда», что выполняются равенства

Рассмотрим прямые и составим три уравнения из соответствующих коэффициентов: . Из каждого уравнения следует, что , следовательно, данные прямые совпадают.

И действительно, если все коэффициенты уравнения умножить на –1 (сменить знаки), и все коэффициенты уравнения сократить на 2, то получится одно и то же уравнение: – вспоминаем, что это «эталонный» вид общего уравнения прямой.

Второй случай, когда прямые параллельны:

2) Две прямые параллельны тогда и только тогда, когда их коэффициенты при переменных и пропорциональны: , но

В качестве примера рассмотрим прямые . Сначала проверяем пропорциональность соответствующих коэффициентов при переменных :

Однако совершенно очевидно, что .

Вывод:

И третий случай, когда прямые пересекаются:

3) Две прямые пересекаются, тогда и только тогда, когда их коэффициенты при переменных и НЕ пропорциональны, то есть НЕ существует такого значения «лямбда», чтобы выполнялись равенства

Так, оставим систему для прямых :

Из первого уравнения следует, что , а из второго уравнения: , значит, система несовместна (нет решений). Таким образом, коэффициенты при переменных не пропорциональны.

Вывод: прямые пересекаются

В практических задачах можно использовать только что рассмотренную схему решения, но существует и более «цивилизованная» упаковка:

Задача 74

Выяснить взаимное расположение прямых:

Решение основано на исследовании направляющих векторов прямых:

а) Из уравнений найдём направляющие векторы прямых: .

Вычислим определитель, составленный из координат данных векторов:
, значит, векторы не коллинеарны и прямые пересекаются.

Вопрос: всё ли вам понятно? Если нет, то используйте три ссылки выше. Ну а остальные перепрыгивают камень и следуют дальше, прямо к Кащею Бессмертному =)

б) Найдем направляющие векторы прямых :
– прямые имеют один и тот же направляющий вектор, значит, они либо параллельны, либо совпадают (тут и определитель считать не надо).

Очевидно, что коэффициенты при переменных пропорциональны и .

Выясним, справедливо ли равенство :

Таким образом,

в) Найдем направляющие векторы прямых :

Вычислим определитель, составленный из координат данных векторов:
, следовательно, направляющие векторы коллинеарны и прямые либо параллельны, либо совпадают.

Коэффициент пропорциональности «лямбда» можно узнать прямо соотношения коллинеарных направляющих векторов . Впрочем, можно и через коэффициенты самих уравнений: .

Теперь выясним, справедливо ли равенство . Оба свободных члена нулевые, поэтому:

Полученное значение удовлетворяет данному уравнению (ему удовлетворяет вообще любое число).

Таким образом, прямые совпадают.

Ответ:

Очень скоро вы научитесь (или даже уже научились) решать рассмотренную задачу устно и буквально в считанные секунды – присмотрелись к уравнениям, и всё понятно.

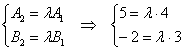
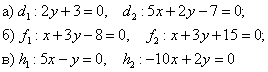
2.5.2. Как найти прямую, параллельную данной?

2.4. Параметрические уравнениЯ прямой

| Оглавление |

Автор: Aлeксaндр Eмeлин