|
Ваш репетитор, справочник и друг!
|
2.4. Параметрические уравнениЯ прямой
Если известна некоторая точка В чём смысл? Параметр Задача 71 Составить параметрические уравнения прямой по точке Решение закончилось, не успев начаться: Как найти точки прямой? Возьмём какое-нибудь значение параметра, например, Обратная задача: как проверить, будет ли точка Из обоих уравнений следует, что Рассмотрим более содержательные примеры: Задача 72 Составить параметрические уравнения прямой Решение: по условию прямая задана в общем виде. Для того чтобы составить параметрические уравнения прямой, нужно знать её направляющий вектор и какую-нибудь точку. Найдём направляющий вектор: Теперь нужно найти какую-нибудь точку, принадлежащую прямой, здесь проще всего обнулить «иксовую» координату Составим параметрические уравнения прямой: Ответ: И небольшое творческие задание для самостоятельного решения. Задача 73 Составить параметрические уравнения прямой, если известна принадлежащая ей точка Решение и ответ в конце книги. Укрепляем заложенный геометрический фундамент простейшими задачами с прямой:
|
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Аналитическая геометрия для «чайников»
Аналитическая геометрия для «чайников»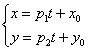
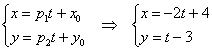
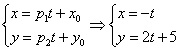
 2.5.1. Взаимное расположение двух прямых
2.5.1. Взаимное расположение двух прямых 2.3. Уравнение прямой в отрезках
2.3. Уравнение прямой в отрезках