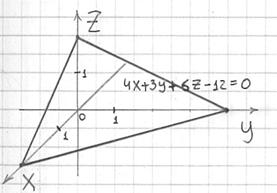
5.1.5. Уравнение плоскости в отрезках

Важнейшая прикладная разновидность. Если все коэффициенты общего уравнения плоскости отличны от нуля, то оно представимо в виде , который называется уравнением плоскости в отрезках. Очевидно, что плоскость пересекает координатные оси в точках , и большое преимущество такого уравнения состоит в лёгкости построения чертежа:

Задача 128

Построить плоскость

Решение: составим уравнение плоскости в отрезках. Перебросим свободный член направо и разделим обе части на 12:

,
Делаем дроби трёхэтажными:

Именно так! – ведь знаменатели могут оказаться и дробными. Но в данном случае всё разделилось нацело:

Таким образом, плоскость проходит через точки . В целях самоконтроля координаты каждой точки устно подставим в исходное уравнение . После чего выполним чертёж:

В отличие от предыдущих примеров здесь фрагмент плоскости изображается в виде треугольника, который, как я уже отмечал, может «прорисоваться» в любом из 8 октантов.
Уравнение содержит длины трёх отрезков, которые «исходят» из начала координат и однозначно определяют плоскость (отсюда и название уравнения).

Задание для тренировки:

Задача 129

Построить плоскость

После чего возвращаемся к аналитике.

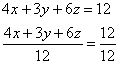
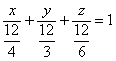
5.2.1. Уравнение плоскости по точке и двум неколлинеарным векторам

5.1.4. Как построить плоскость?

| Оглавление |