5.2.1. Как составить уравнение плоскости
по точке и двум неколлинеарным векторам?
Конструировать уравнение будем с помощью векторов и точек. Их должно быть как можно меньше, но достаточно, чтобы однозначно определить плоскость. Одним словом, красивая математическая лаконичность.
Казалось бы, плоскость можно однозначно определить с помощью двух неколлинеарных векторов. Но нет – векторы свободны и бродят по всему пространству, поэтому ещё нужна фиксированная точка:
Уравнение плоскости, которая проходит через точку 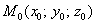 параллельно неколлинеарным векторам параллельно неколлинеарным векторам 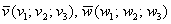 , выражается формулой: , выражается формулой:

! Примечание: под выражением «вектор параллелен плоскости» подразумевается, что вектор можно отложить и в самой плоскости. Для наглядности я буду откладывать векторы прямо в плоскости.
Принципиально ситуация выглядит так:
 Обратите внимание, что точка и два коллинеарных вектора не определят плоскость однозначно (они будут «вертеться» вокруг точки и зададут целый «пучок» плоскостей). Обратите внимание, что точка и два коллинеарных вектора не определят плоскость однозначно (они будут «вертеться» вокруг точки и зададут целый «пучок» плоскостей).
Задача 130
Составить уравнение плоскости по точке 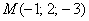 и неколлинеарным векторам и неколлинеарным векторам 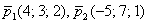 . .
Решение: искомое уравнение составим по формуле:
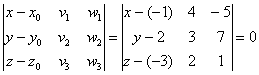
Определитель удобнее всего раскрыть по первому столбцу:

Раскрываем определители второго порядка:
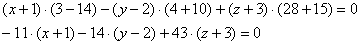
На первом месте у нас нарисовался знак «минус», и хорошим тоном считается его убрать (точно так же, как и у общего уравнения «плоской» прямой).
Меняем у каждого слагаемого знак и проводим дальнейшие упрощения:

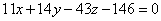 , сократить здесь ничего нельзя, поэтому: , сократить здесь ничего нельзя, поэтому:
Ответ: 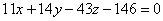
Как проверить задание? Для проверки пока не хватает информации, но мы обязательно выполним её чуть позже. Решаем самостоятельно:
Задача 131
Составить уравнение плоскости по векторам  и принадлежащей ей точке и принадлежащей ей точке 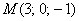 . .
Кстати, если векторы коллинеарны, то и на этот случай есть корректный ответ ;)
 5.2.2. Как составить уравнение плоскости по трём точкам? 5.2.2. Как составить уравнение плоскости по трём точкам?
 5.1.5. Уравнение плоскости в отрезках 5.1.5. Уравнение плоскости в отрезках
| Оглавление |
|