5.2.2. Как составить уравнение плоскости по трём точкам?

Этот способ промелькнул в самом начале главы и уже громко стучится в дверь. Любые ли три точки пространства задают плоскость? Нет. Во-первых, точки должны быть различными. А во-вторых, они не должны лежать на одной прямой (сразу все три).

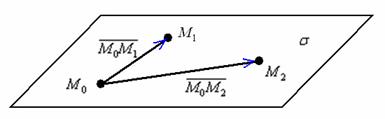
Уравнение плоскости, проходящей через три различные точки , которые не лежат на одной прямой, можно составить по формуле:

На самом деле это разновидность предыдущего способа, смотрим на картинку:

Если известны три различные точки, не лежащие на одной прямой, то легко найти два неколлинеарных вектора, параллельных этой плоскости:

То есть, наша формула фактически совпадает с формулой предыдущего параграф, и чтобы не уснуть от скуки, предлагаю раскрутить задачи-«шарады»:

Задача 132

Составить уравнение плоскости по точкам .

Решение: по соответствующей формуле:

Вот теперь и аналитически видно, что всё дело свелось к координатам двух векторов. Раскрываем определитель по первому столбцу и находим уравнение плоскости:

, больше ничего упростить нельзя, записываем:

Ответ:

Проверка напрашивается сама собой – в полученное уравнение плоскости нужно подставить координаты каждой точки. Если хотя бы одна из трёх точек «не подойдёт», ищите ошибку.

Для «мёртвого» зачёта всегда выполняйте проверку – мысленно, на черновике или прямо на чистовике!!! Не устану повторять этот вечно живой и актуальный призыв.

Задача 133

Составить уравнение плоскости, проходящей через точки и начало координат.

Выберите наиболее выгодный способ решения ;)

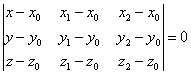
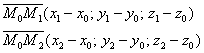
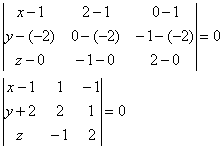
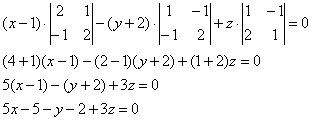
5.2.3. Вектор нормали плоскости (нормальный вектор)

5.2.1. Уравнение плоскости по точке и двум неколлинеарным векторам

| Оглавление |

Автор: Aлeксaндр Eмeлин