|
Ваш репетитор, справочник и друг!
|
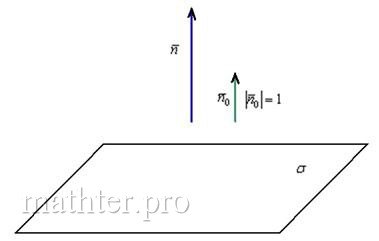
5.2.3. Вектор нормали плоскости (нормальный вектор)Вектор нормали плоскости – это вектор, который перпендикулярен данной плоскости. Очевидно, что у любой плоскости бесконечно много нормальных векторов. Но для решения задач нам будет хватать и одного: если плоскость задана общим уравнением Просто до безобразия! – всё, что нужно сделать – это «снять» коэффициенты из уравнения плоскости. И чтобы хоть как-то усложнить практику рассмотрим тоже простую, но очень важную задачу, которая часто встречается, причём, не только в геометрии: Задача 134 Найти единичный нормальный вектор плоскости Решение: принципиально ситуация выглядит так: Сначала из уравнения плоскости «снимем» вектор нормали: И эту задачку мы уже решали: для того чтобы найти единичный вектор Вычислим длину вектора нормали: Таким образом: Контроль: Ответ: Вспоминаем, что координаты этого вектора – есть в точности направляющие косинусы вектора И, как говорится, обещанного три страницы ждут :) – вернёмся к Задаче 130, чтобы выполнить её проверку. Напоминаю, что там требовалось построить уравнение плоскости по точке Проверяем: Во-первых, подставим координаты точки На втором шаге из уравнения плоскости «снимаем» вектор нормали: Вывод: уравнение плоскости найдено правильно. В ходе проверки я фактически процитировал следующее утверждение теории: вектор Итак, с «выуживанием» нормального вектора разобрались, теперь ответим на противоположный вопрос:
|
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Аналитическая геометрия для «чайников»
Аналитическая геометрия для «чайников»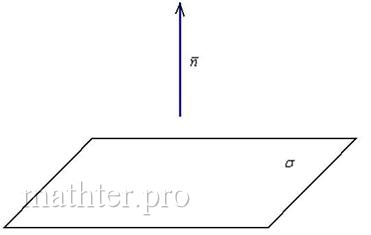
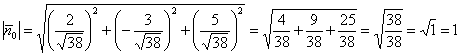 , ОК
, ОК 5.2.4. Как составить уравнение плоскости по точке и вектору нормали?
5.2.4. Как составить уравнение плоскости по точке и вектору нормали? 5.2.2. Как составить уравнение плоскости по трём точкам?
5.2.2. Как составить уравнение плоскости по трём точкам?