5.2.4. Как составить уравнение плоскости
по точке и вектору нормали?
Вытяните вперёд руку и мысленно зафиксируйте произвольную точку пространства… прямо, как Владимир Ильич Ленин :). Очевидно, что эта конструкция тоже однозначно определяет плоскость:
Уравнение плоскости, проходящей через точку 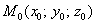 перпендикулярно вектору перпендикулярно вектору 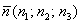 , в декартовой системе координат выражается формулой: , в декартовой системе координат выражается формулой:
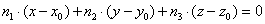
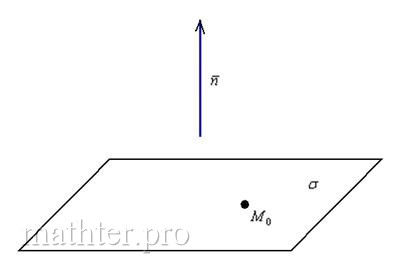
Выглядит значительно привлекательнее, чем предыдущие мытарства. И поэтому если в какой-то задаче вам известен вектор нормали, то, конечно же, уравнение выгодно составлять через него.
Но ещё раз обращаю внимание, что формулы, касаемые вектора нормали, работают лишь в декартовой системе координат, но не в общем аффинном случае.
Задача 135
Составить уравнение плоскости по точке 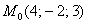 и вектору нормали и вектору нормали 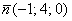 . .
Решение: используем формулу 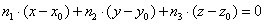 : :
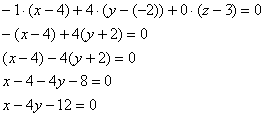
Ответ: 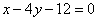
Проверка выполняется очень легко:
1) Из полученного уравнения 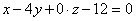 «снимаем» вектор нормали: «снимаем» вектор нормали: 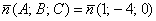 – всё хорошо, полученный вектор совпал с вектором из условия (в ряде случаев может получиться коллинеарный вектор). – всё хорошо, полученный вектор совпал с вектором из условия (в ряде случаев может получиться коллинеарный вектор).
2) Подставим координаты точки 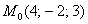 в уравнение плоскости: в уравнение плоскости:
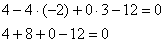
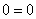 – верное равенство, значит, точка – верное равенство, значит, точка 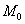 принадлежит данной плоскости. принадлежит данной плоскости.
Вывод: уравнение плоскости найдено правильно.
Пример настолько прозрачен, что хочется немного завуалировать условие:
Задача 136
Найти уравнение плоскости, проходящей через точку 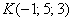 перпендикулярно оси абсцисс. перпендикулярно оси абсцисс.
Это задача для самостоятельного решения. Просто, но со вкусом.
И тема получает закономерное продолжение, рассмотрим простейшие задачи с плоскостью:
 5.3.1. Как найти плоскость, параллельную данной? 5.3.1. Как найти плоскость, параллельную данной?
 5.2.3. Вектор нормали плоскости (нормальный вектор) 5.2.3. Вектор нормали плоскости (нормальный вектор)
| Оглавление |
|