|
Ваш репетитор, справочник и друг!
|
5.3.4. Взаимное расположение двух плоскостейС параллельными плоскостями мы только что столкнулись и сейчас разовьём тему. Рассмотрим две плоскости пространства, заданные общими уравнениями: Они могут: 1) совпадать; 2) быть параллельными: 3) пересекаться по некоторой прямой «эль»: По пунктам: 1) Совпадающие плоскости
Две плоскости совпадают, тогда и только тогда, когда их соответствующие коэффициенты пропорциональны, то есть, существует такое число «лямбда», что выполняются равенства Рассмотрим плоскости Из каждого уравнения системы следует, что 2) Параллельные плоскости
Две плоскости параллельны тогда и только тогда, когда их коэффициенты при переменных На практике первые три коэффициента часто банально попарно совпадают Убедимся, что эти прямые действительно параллельны. Составим пропорцию из соответствующих коэффициентов Из первых трёх уравнений следует, что 3) Пересекающиеся плоскостиИ третий, самый распространённый случай, когда две плоскости пересекаются по некоторой прямой Попутно заметим важный факт: если плоскости пересекаются, то система линейных уравнений Но о пространственной прямой позже. В качестве примера рассмотрим плоскости Из первых двух уравнений следует, что
|
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Аналитическая геометрия для «чайников»
Аналитическая геометрия для «чайников»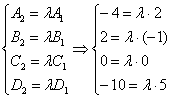
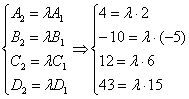
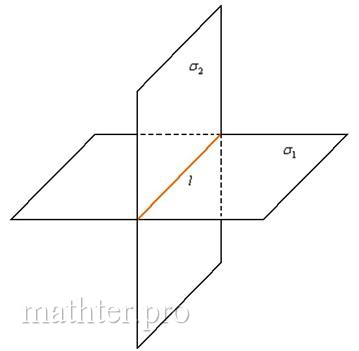 Две плоскости пересекаются тогда и только тогда, когда их коэффициенты при переменных
Две плоскости пересекаются тогда и только тогда, когда их коэффициенты при переменных 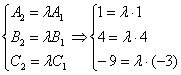
 5.3.5. Как найти угол между плоскостями?
5.3.5. Как найти угол между плоскостями? 5.3.3. Как найти расстояние между плоскостями?
5.3.3. Как найти расстояние между плоскостями?