Ваш репетитор, справочник и друг!

Аналитическая геометрия для «чайников»

5.4.3. Параметрические уравнения прямой

Важнейший вид! Да, параметрические уравнения, конечно, не альфа и омега пространственной геометрии, но «рабочая лошадка» многих задач. Причём, этот вид уравнений часто применяется неожиданно, и я бы сказал, изящно.

Если известна точка , принадлежащая прямой, и направляющий вектор данной прямой, то параметрические уравнения этой прямой задаются системой:

Всё проще пареной репы, поэтому придётся приперчить задачу:

Задача 149

Составить параметрические уравнения следующих прямых:

а)

б)

в)

Решение: прямые заданы каноническими уравнениями и на первом этапе следует найти какую-нибудь точку, принадлежащую прямой, и её направляющий вектор.

а) Из уравнений «снимаем» точку и направляющий вектор: . Точку можно выбрать и другую (как это сделать – рассказано после Задачи 143), но лучше взять самую очевидную. Кстати, во избежание ошибок, всегда подставляйте её координаты в уравнения.

Составим параметрические уравнения данной прямой:

Одно из удобств состоит в том, с помощью этих уравнений легко находить как раз другие точки прямой. Например, найдём точку , координаты которой, скажем, соответствуют значению параметра :

Таким образом:

б) Рассмотрим канонические уравнения . Выбор точки здесь несложен, но коварен: – будьте внимательны, не перепутайте координаты!!!. Как «вытащить» направляющий вектор? Можно порассуждать, чему параллельна данная прямая, а можно использовать простой формальный приём: в пропорции находятся «игрек» и «зет», поэтому запишем направляющий вектор , а на оставшееся место поставим ноль: …, зря я об этом рассказал, теперь расслабитесь :)

Составим параметрические уравнения прямой:

в) Перепишем уравнения в виде , то есть «зет» может быть любым. А если любым, то пусть, например, . Таким образом, точка принадлежит данной прямой. Для нахождения направляющего вектора используем следующий формальный приём: в исходных уравнениях находятся «икс» и «игрек», и в направляющем векторе на этих местах записываем нули: . На оставшееся место ставим единицу: . Вместо единицы подойдёт любое число, кроме нуля, но единица лаконичнее всего.

Запишем параметрические уравнения прямой:

И в академичном стиле тут ещё можно записать ответ, в котором под пунктами «а», «бэ» и «вы» перечислить полученные уравнения.

Аналогичное задание для самостоятельного решения:

Задача 150

Составить параметрические уравнения следующих прямых:

а) ;

б) ;

в) прямая проходит через точки .

Решения в конце книги. Полученные вами ответы могут несколько отличаться от моих ответов, дело в том, что параметрические уравнения можно записать не единственным способом. Важно, чтобы ваши и мои направляющие векторы были коллинеарны, и ваша точка «подходила» к моим уравнениям (ну, или наоборот, моя точка – к вашим уравнениям :).

Как ещё можно задать прямую в пространстве? Хочется что-нибудь придумать с вектором нормали. Но тут ничего не получится – у пространственной прямой нормальные векторы могут смотреть совершенно в разные стороны.

Ещё один способ уже несколько раз «проскакивал» ранее:

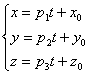
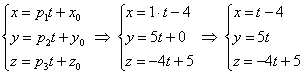
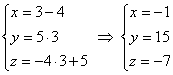
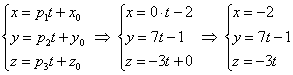
5.4.4. Прямая, заданная пересечением двух плоскостей

5.4.2. Как составить уравнения прямой по двум точкам?

| Оглавление |

Автор: Aлeксaндр Eмeлин