5.6.6. Прямая параллельна плоскости

Таких задач я отыскал совсем немного и решил приютить сироту:

Задача 164

Даны скрещивающиеся прямые . Через прямую провести плоскость, параллельную прямой .

Решение: задачка простая, но всё равно выполним схематический чертёж:

Итак, нам нужно составить уравнение плоскости , которая проходит через прямую параллельно второй прямой.

И прямо из рисунка видно, что для этого подойдёт любая точка прямой и её направляющий вектор. Их легко «снять» из уравнений прямой:

По условию плоскость должна быть параллельна прямой , а значит, и её направляющему вектору . Так как прямые скрещиваются, то их направляющие векторы будут не коллинеарны.

Уравнение плоскости составим по точке и двум неколлинеарным векторам :

Ответ:

Как выполнить проверку? Устно. «Снимаем» из уравения плоскости вектор нормали и с помощью скалярного произведения убеждаемся, что он ортогонален направляющим векторам прямых. Тренируем устный счёт!

Аналогично можно составить уравнение плоскости , которая проходит через прямую параллельно прямой . Решение будет точно таким же, изменится только точка – необходимо взять какую-нибудь точку, принадлежащую второй прямой. Очевидно, что данные плоскости будут параллельны: .

По ходу создания этой главы мне совершенно случайно попалась на глаза одна методичка для студентов-заочников, где среди прочих заданий, как раз есть десять задач по аналитической геометрии в пространстве. Находка оказалась очень своевременной и удачной, поскольку предоставила отличную возможность прикинуть, насколько пОлно я рассмотрел всю тему. И, конечно же, предложить вам эти задачи для самопроверки:

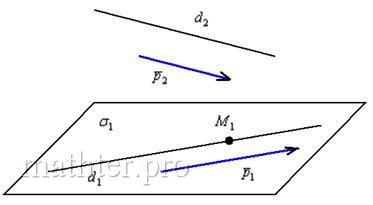
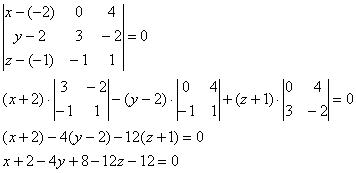
5.6.7. Добро пожаловать в «реальные боевые условия»!

5.6.5. Прямая перпендикулярна плоскости

| Оглавление |

Автор: Aлeксaндр Eмeлин