4.4. Оценка генеральной дисперсии нормально распределенной совокупности
Этот интервал можно построить несколькими способами, которые я постараюсь уместить буквально в пару страниц. Продолжаем
решать ту же задачу об измерениях:
Пример 23
По 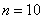 равноточным измерениям найдено
исправленное среднее квадратическое отклонение равноточным измерениям найдено
исправленное среднее квадратическое отклонение 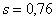 .
Предполагая, что результаты измерений распределены нормально, построить доверительный интервал для оценки истинного значения .
Предполагая, что результаты измерений распределены нормально, построить доверительный интервал для оценки истинного значения 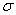 (генерального стандартного отклонения) с
надёжностью (генерального стандартного отклонения) с
надёжностью 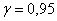 . .
Обратите внимание, что для решения этой задачи нам не обязательно знать выборочную среднюю (хотя в Примере 13 мы её нашли).
Способ первый. Доверительный интервал для оценки неизвестной дисперсии 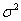 нормальнойгенеральной совокупности определяется следующим
образом (не пугаемся): нормальнойгенеральной совокупности определяется следующим
образом (не пугаемся):
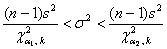 , где , где 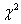 – распределение «хи-квадрат» (ещё один скелет в шкафу:)), а – распределение «хи-квадрат» (ещё один скелет в шкафу:)), а 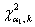 , , 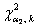 –
критические значения, вычисленные для –
критические значения, вычисленные для 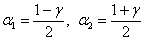 и и 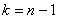 . Что это всё значит, я рассказывать тоже не буду
J. . Что это всё значит, я рассказывать тоже не буду
J.
Данный интервал с вероятностью 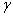 (надёжностью) накрывает истинное значение генеральной дисперсии (надёжностью) накрывает истинное значение генеральной дисперсии 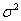 . А если из всех частей неравенства извлечь корни, то
получим соответствующий интервал для оценки генерального стандартного отклонения: . А если из всех частей неравенства извлечь корни, то
получим соответствующий интервал для оценки генерального стандартного отклонения:
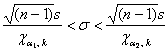
Значения 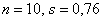 известны, осталось разобраться с
нижним этажом. Вычислим известны, осталось разобраться с
нижним этажом. Вычислим 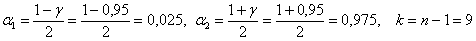 и по таблице критических значений распределения и по таблице критических значений распределения 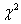 либо по макету (пункт 3б)
найдём: либо по макету (пункт 3б)
найдём:
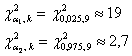
В результате:
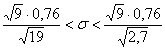 – не забываем извлечь корни из
знаменателей! – не забываем извлечь корни из
знаменателей!
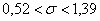 – таким образом, с вероятностью – таким образом, с вероятностью 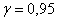 можно утверждать, что данный интервал накроет
генеральное стандартное отклонение можно утверждать, что данный интервал накроет
генеральное стандартное отклонение 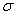 . .
Полученный интервал асимметричен относительно выборочного значения 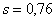 , и его широкий диапазон объясним малым объёмом выборки – велика вероятность, что при
10 измерениях значение «эс» действительно далеко от истинного значения «сигма». , и его широкий диапазон объясним малым объёмом выборки – велика вероятность, что при
10 измерениях значение «эс» действительно далеко от истинного значения «сигма».
Способ второй, более простой. Он состоит в построении симметричного интервала по формуле:
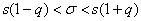 , где значение , где значение 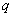 отыскивается по соответствующей таблице. отыскивается по соответствующей таблице.
Согласно таблице, доверительной вероятности 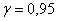 и объёму и объёму 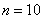 соответствует значение соответствует значение 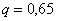 , таким образом: , таким образом:
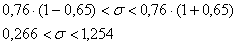
В результате мы получили примерно такой же широкий интервал. Для малых выборок может даже получиться 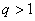 , в таких случаях принимают ещё более грубую интервальную оценку: , в таких случаях принимают ещё более грубую интервальную оценку:
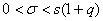
Ответ: 1) 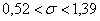 , 2) , 2) 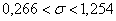 . .
Как и для распределения Стьюдента, при увеличении 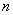 распределение хи-квадрат стремится к нормальному распределению, и уже
при распределение хи-квадрат стремится к нормальному распределению, и уже
при 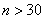 можно использовать приближенную
формулу: можно использовать приближенную
формулу:
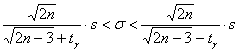 , где коэффициент доверия , где коэффициент доверия 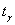 , который определяется из знакомого лапласовского соотношения , который определяется из знакомого лапласовского соотношения 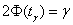 . .
Иногда встречаются обратная задача – по известной точности оценки (фактически по известному интервалу) найти
доверительную вероятность 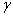 . Иногда требуется
построить одностороннюю оценку. Но ввиду их исключительного «иногда», я передаю привет студентам Московского института
статистики и продолжаю :) Точнее, предлагаю продолжить вам: . Иногда требуется
построить одностороннюю оценку. Но ввиду их исключительного «иногда», я передаю привет студентам Московского института
статистики и продолжаю :) Точнее, предлагаю продолжить вам:
Пример 24
В результате обработки экспериментальных данных объёма 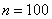 получены следующие выборочные характеристики: получены следующие выборочные характеристики: 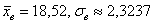 . В предположении о нормальном распределении генеральной совокупности, с надёжностью . В предположении о нормальном распределении генеральной совокупности, с надёжностью 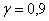 определить доверительные интервалы: определить доверительные интервалы:
1) для оценки неизвестной генеральной средней 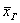 ; ;
2) для оценки генерального среднего квадратического отклонения 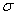 двумя способами – с помощью распределения хи-квадрат: двумя способами – с помощью распределения хи-квадрат: 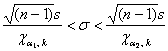 и приближённо, по формуле и приближённо, по формуле 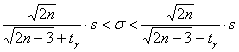 , где , где 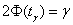 . .
Заметьте, что здесь «плакал» лёгкий способ построения интервала 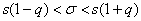 , так как в стандартной таблице отсутствуют значения
для , так как в стандартной таблице отсутствуют значения
для 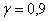 . .
А рассчитывать значения «ку» программным способом – геморрой ещё тот. Краткое решение и примерный образец оформления
задачи в конце книги. Далее по курсу:
 4.5. Повторная и бесповторная выборка 4.5. Повторная и бесповторная выборка
 4.3. Оценка генеральной средней нормально распределенной совокупности 4.3. Оценка генеральной средней нормально распределенной совокупности
| Оглавление |
|

 Математическая статистика – краткий курс для начинающих
Математическая статистика – краткий курс для начинающих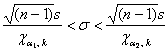
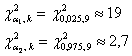
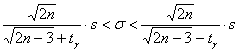 , где коэффициент доверия
, где коэффициент доверия 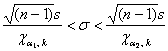 и приближённо, по формуле
и приближённо, по формуле 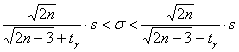 , где
, где  4.5. Повторная и бесповторная выборка
4.5. Повторная и бесповторная выборка 4.3. Оценка генеральной средней нормально распределенной совокупности
4.3. Оценка генеральной средней нормально распределенной совокупности