Ваш репетитор, справочник и друг!

Математическая статистика – краткий курс для начинающих

4.3. Оценка генеральной средней нормально распределенной совокупности

Если вы не знаете, что такое нормальное распределение, то это, конечно, большое упущение – обязательно ознакомьтесь с материалом по ссылке. И мы сразу разберём «заезженную» задачу, которую предлагают даже студентам-гуманитариям:

Пример 19

Известно, что генеральная совокупность распределена нормально со средним квадратическим отклонением . Найти доверительный интервал для оценки математического ожидания с надежностью 0,95, если выборочная средняя , а объем выборки .

Прежде всего, обращаю ваше внимание на принципиальный момент: здесь

4.3.1. Известно стандартное отклонение генеральной совокупности

Дело в том, что в похожих задачах оно бывает и не известно, и тогда решение будет отличаться! Этот случай тоже будет. А сейчас решение таково, разбираемся в ситуации:

– из генеральной совокупности проведена выборка в попугаев и по её результатам найдена выборочная средняя: (средний рост птицы).

Выборочная средняя – это точечная оценка неизвестной нам генеральной средней . Как отмечалось выше, недостаток точечной оценки состоит в том, что она может оказаться далёкой от истины. И по условию, требуется найти интервал , который с вероятностью накроет истинное значение .

Именно так! Здесь некорректно говорить, что «истинное значение попадёт в этот интервал». Генеральная средняя – это конкретное (пусть и не известное нам) значение, и оно не может никуда «попасть». В разных выборках мы будем получать разные значения и разные доверительные интервалы, которые могут лишь накрыть генеральную среднюю. А могут и не накрыть (некоторые из них).

Найдём точность оценки, она рассчитывается по формуле , где – так называемый коэффициент доверия. Этот коэффициент отыскивается из соотношения , где – функция Лапласа.

По условию, , следовательно:

И по таблице значений функции Лапласа либо пользуясь приложенным к курсу расчётным макетом (пункт 1*), выясняем, что значению соответствует аргумент .

Таким образом, точность оценки:

и искомый доверительный интервал:

Этот интервал с вероятностью (надёжностью) накрывает истинное генеральное значение среднего роста попугая. Но всё же остаётся 5%-ная вероятность того, что генеральная средняя окажется вне найденного интервала.

Ответ: .

И тут возникает светлая мысль уменьшить этот интервал – чтобы получить более точную оценку. Что для этого можно сделать? Давайте посмотрим на формулу .

Очевидно, что чем меньше стандартное отклонение (мера разброса значений), тем уже доверительный интервал. Но это в отдельно взятой задаче ни на что не влияет – ведь нам известно конкретное значение и изменить его невозможно.

Поэтому для уменьшения «дельты» можно уменьшить коэффициент доверия, например, вместо рассмотреть и тогда , в результате чего доверительный интервал – действительно стал в 2 раза короче. Но засада в том, что упала и доверительная вероятность:

пользуясь таблицей значений функции Лапласа либо расчётным макетом (пункт 1), находим: – то есть о том, что этот более узкий интервал накроет генеральную среднюю, мы теперь можем утверждать лишь с вероятностью 68,26%. Что, конечно, неудовлетворительно, для серьёзного статистического исследования.

Поэтому для уменьшения доверительного интервала (при том же значении ) остаётся увеличивать объём выборки . Что совершенно понятно и без формулы , ведь чем больше объём выборки, тем точнее она характеризует генеральную совокупность (при прочих равных условиях). Об объёме выборки мы поговорим позже, ну а пока творческая задача для самостоятельного решения:

Пример 20

По результатам выборочного исследования объектов найдена выборочная средняя .

1) С какой вероятностью можно утверждать, что генеральная средняя отличается от найденного значения не более чем на 3, если известно, что генеральная совокупность распределения нормально с дисперсией 400?

2) Определить доверительный интервал, который с надежностью накроет истинное значение генеральной средней.

Образец в конце книги, таблица либо расчётный макет (пункты 1 и 1*) в помощь.

И тут, наверное, у вас назрели вопросы – а откуда известно, что генеральная совокупность распределена нормально, и тем более, откуда известно её стандартное отклонение?

Обычно эта информация известна из предыдущих исследований. Классический пример – измерительный прибор. Очевидно, что его случайные погрешности удовлетворяют условию теоремы Ляпунова, а значит, распределены нормально. Кроме того, производитель, как правило, тестирует прибор, и указывает в его паспорте стандартное отклонение случайной погрешности, которое можно принять за .

Но если установить нормальность распределения достаточно просто (в том числе статистическими методами), то с генеральным значением всё сложнее – зачастую вычислить его трудно или невозможно. В такой ситуации остаётся ориентироваться на исправленную выборочную дисперсию и решение несколько изменится. Возвращаемся к нашей любимой задаче:

Пример 21

В результате 10 независимых измерений некоторой величины , выполненных с одинаковой точностью, полученные опытные данные, которые представлены в таблице:

Предполагая, что результаты измерений подчинены нормальному закону распределения вероятностей, оценить истинное значение величины при помощи доверительного интервала, покрывающего это значение с вероятностью 0,95.

Обратите внимание, что здесь речь идёт уже не о погрешностях прибора, а об измерениях, и помимо технических, велико влияние других, в частности, человеческого фактора, особенно, если вы используете махрово-аналоговый инструмент – что-нибудь вроде механического секундомера или линейки.

Решение следует начать с вычисления выборочных характеристик, и задача облегчается тем, что в Примере 13 они уже вычислены: . По условию, требуется оценить генеральную совокупность (а именно, параметр ), и поэтому дисперсию нужно обязательно поправить:
– несмещённая оценка неизвестной генеральной дисперсии . И нас будет интересовать несмещённая оценка генерального стандартного отклонения :
– исправленное среднее квадратическое отклонение.

Теперь построим доверительный интервал для оценки истинного (генерального) значения величины .

4.3.2. Если генеральная дисперсия нормального распределения не известна

то этот интервал строится по похожей формуле:

, с той поправкой, что коэффициент доверия рассчитывается с помощью распределения Стьюдента. Я не буду рассказывать об этом распределении и ограничусь технической стороной вопроса.

Значение можно найти с помощью таблицы значений распределения Стьюдента, в частности популярна таблица, специально адаптированная для данной задачи*. И, согласно таблице, доверительной вероятности и объёму выборки соответствует коэффициент доверия:

* в таблице, которую можно встретить чаще, приводятся значения для так называемого уровня значимости и для количества степеней свободы .

Другой, более универсальный способ – воспользоваться Экселем, и чтобы далеко не ходить, я добавил этот функционал в расчётный макет: ищем пункт 2б, забиваем значения , и получаем «на выходе» .

Вычислим точность оценки:

Таким образом, искомый доверительный интервал:

– данный интервал с вероятностью накрывает истинное генеральное значение измеряемой величины .

Ответ:

Для самостоятельного решения:

Пример 22

На основании испытаний установлено, что в среднем для изготовления шавермы полупроводникового диода требуется секунд, а исправленное среднее квадратическое отклонение составляет секунд. Предположив, что время изготовления диода есть нормальная случайная величина, определить с надежностью доверительный интервал для оценки среднего времени изготовления диода

Краткое решение в конце книги, таблица или макет (пункт 2б) – в помощь.

Итак, что главное в разобранных задачах? Главное, обратить внимание, генеральное ли нам дано отклонение или исправленное выборочное . От этого зависит, какую формулу нужно использовать, эту:
, где ,
или эту:
, где отыскивается с помощью распределения Стьюдента.

При увеличении объёма выборки , распределение Стьюдента стремится к нормальному распределению, и поэтому уже при во 2-м случае допускается нахождение с помощью того же соотношения . Но я бы не рекомендовал так делать. Потому что если дано , то предполагается, что решать нужно именно через «Стьюдента», и при наличии Экселя с этим никаких проблем – можно рассчитать любые значения, которые отсутствуют в таблицах.

Коварные авторы могут предложить «простое» выборочное отклонение , и тогда его следует поправить по формуле: , которая следует из соотношения дисперсий: . Иногда бывает предложена и дисперсия (та или иная). Именно здесь нужно проявлять аккуратность, сами же вычисления достаточно примитивны.

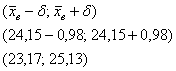
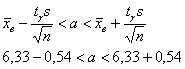
4.4. Оценка генеральной дисперсии нормально распределенной совокупности

4.2 Интервальная оценка

| Оглавление |