4. Статистические оценки параметров генеральной совокупности
Вспомним основной метод математической статистики. Он состоит в том, что для изучения генеральной совокупности объёма 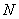 из неё производится выборка объёма из неё производится выборка объёма 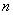 , которая хорошо характеризует всю совокупность (свойство представительности). И на основании исследования этой выборочной совокупности мы с некоторой достоверностью можем оценить генеральные характеристики. Само собой, чем выше достоверность – тем лучше, тем качественнее исследование. Этому вопросу и посвящена данная глава. , которая хорошо характеризует всю совокупность (свойство представительности). И на основании исследования этой выборочной совокупности мы с некоторой достоверностью можем оценить генеральные характеристики. Само собой, чем выше достоверность – тем лучше, тем качественнее исследование. Этому вопросу и посвящена данная глава.
Чаще всего требуется выявить закон распределения генеральной совокупности (о чём пойдёт речь позже) и оценить его важнейшие числовые параметры, такие как генеральная средняя 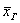 , генеральная дисперсия , генеральная дисперсия 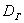 и стандартное отклонение и стандартное отклонение 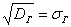 . .
4.1. Точечные оценки
Очевидно, что для оценки этих параметров нужно вычислить соответствующие выборочные значения. Так, выборочная средняя 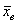 позволяет нам оценить генеральную среднюю позволяет нам оценить генеральную среднюю 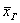 , причём, оценить её точечно. Почему точечно? Потому что , причём, оценить её точечно. Почему точечно? Потому что 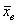 – это отдельно взятое, конкретное значение. Если из той же генеральной совокупности мы будем проводить многократные выборки, то в общем случае у нас будут получаться различные выборочные средние, и каждая из них представляет собой точечную оценку генерального значения – это отдельно взятое, конкретное значение. Если из той же генеральной совокупности мы будем проводить многократные выборки, то в общем случае у нас будут получаться различные выборочные средние, и каждая из них представляет собой точечную оценку генерального значения 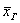 . .
Аналогично, точечной оценкой генеральной дисперсии 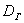 является исправленная выборочная дисперсия является исправленная выборочная дисперсия 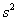 , и соответственно, стандартного отклонения , и соответственно, стандартного отклонения 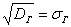 – исправленное стандартное отклонение – исправленное стандартное отклонение 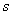 . .
4.2. Интервальная оценка и доверительный интервал
Недостаток точечных оценок состоит в том, что при небольшом объёме выборки (как оно часто бывает), мы можем получать выборочные значения, которые далеки от истины. И в этих случаях логично потребовать, чтобы выборочная характеристика 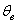 (средняя, дисперсия или какая-то другая) отличалась от своего генерального значения (средняя, дисперсия или какая-то другая) отличалась от своего генерального значения 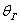 не более чем на некоторое положительное значение не более чем на некоторое положительное значение 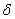 . .
Справка: 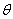 – греческая буква «тета», – греческая буква «тета», 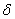 – греческая буква «дельта», вместо «дельты» также используют – греческая буква «дельта», вместо «дельты» также используют 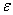 («эпсилон»). («эпсилон»).
Значение 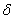 называется точностью оценки, и озвученное выше требование можно записать с помощью модуля: называется точностью оценки, и озвученное выше требование можно записать с помощью модуля: 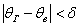
Но статистические методы не позволяют 100%-но утверждать, что рассчитанное значение 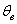 будет удовлетворять этому неравенству – ведь в статистике всегда есть место случайности, когда мы можем «выиграть в лотерею» в плохом смысле этого слова. Таким образом, можно говорить лишь о вероятности будет удовлетворять этому неравенству – ведь в статистике всегда есть место случайности, когда мы можем «выиграть в лотерею» в плохом смысле этого слова. Таким образом, можно говорить лишь о вероятности 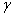 («гамма»), с которой это неравенство осуществится: («гамма»), с которой это неравенство осуществится: 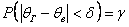 . .
А теперь я раскрою модуль:
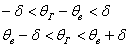
и сформулирую суть:
Интервал 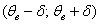 называется доверительным интервалом и представляет собой интервальную оценку генерального значения называется доверительным интервалом и представляет собой интервальную оценку генерального значения 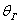 по найденному выборочному значению по найденному выборочному значению 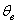 . Данный интервал с вероятностью . Данный интервал с вероятностью 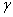 «накрывает» истинное значение «накрывает» истинное значение 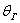 . Эта вероятность называется доверительной вероятностью или надёжностью интервальной оценки. Надёжность «гамма» часто задаётся наперёд, популярные варианты: . Эта вероятность называется доверительной вероятностью или надёжностью интервальной оценки. Надёжность «гамма» часто задаётся наперёд, популярные варианты:
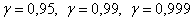 . .
Переходим к конкретике:
 4.3. Оценка генеральной средней нормально распределенной совокупности 4.3. Оценка генеральной средней нормально распределенной совокупности
 3.3. Статистические показатели (итоги по главе) 3.3. Статистические показатели (итоги по главе)
| Оглавление |
|

 Математическая статистика – краткий курс для начинающих
Математическая статистика – краткий курс для начинающих 4.3. Оценка генеральной средней нормально распределенной совокупности
4.3. Оценка генеральной средней нормально распределенной совокупности 3.3. Статистические показатели (итоги по главе)
3.3. Статистические показатели (итоги по главе)