1.5.3. Умножение дробей
Число на дробь умножается просто: 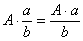 , например: , например: 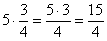 . Оставляем именно в таком виде! Больше ничего с этой дробью делать не
нужно! . Оставляем именно в таком виде! Больше ничего с этой дробью делать не
нужно!
Если перед дробью есть знак «минус» (множитель -1), то его можно отнести к числителю либо знаменателю: 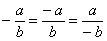 . Это бывает удобно или даже необходимо при решении некоторых задач. Так, у дроби . Это бывает удобно или даже необходимо при решении некоторых задач. Так, у дроби 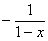 минус выгодно снести вниз, чтобы раскрыть скобки и записать
дробь более компактно: минус выгодно снести вниз, чтобы раскрыть скобки и записать
дробь более компактно: 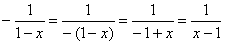 . .
Дробь на дробь тоже умножается просто: 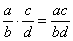 , например: , например:
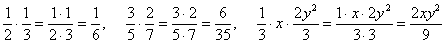 . .
Перед тем, как перемножать числители / знаменатели, нужно посмотреть, а нельзя ли что-нибудь сразу сократить? Это более рациональный
метод вычислений:
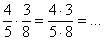 – и здесь вместо перемножения – и здесь вместо перемножения 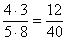 удобно сразу же сократить числитель и знаменатель на четыре: удобно сразу же сократить числитель и знаменатель на четыре: 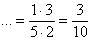
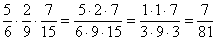 – а здесь перед перемножением удалось сократить на 5 и на 2.
Множители-единицы на чистовике можно не рисовать, это я для понимания. – а здесь перед перемножением удалось сократить на 5 и на 2.
Множители-единицы на чистовике можно не рисовать, это я для понимания.
Далее. Степень. Тоже очевидное правило, которое следует из определения степени: чтобы возвести
дробь в степень, нужно возвести в эту степень числитель и знаменатель:
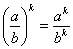 , например: , например: 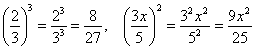 и тому подобное. и тому подобное.
Если дробь отрицательна, а степень чётная, то минус «съедается»: 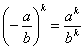 , если же , если же 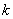 нечётная, то
минус «выскакивает» из-под степени: нечётная, то
минус «выскакивает» из-под степени: 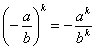 . .
Простейший пример: 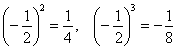
Обратно, для извлечения корня справедливо очевидное правило 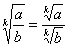 ,
например: ,
например: 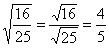 . Если . Если 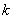 нечётное, то дробь может быть и отрицательной: нечётное, то дробь может быть и отрицательной: 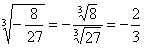 . Но, как вариант: . Но, как вариант: 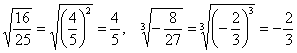 . .
 1.5.4. Деление дробей 1.5.4. Деление дробей
 1.5.2. Как перевести десятичную дробь в обыкновенную? 1.5.2. Как перевести десятичную дробь в обыкновенную?
| Оглавление |
|

 Кратчайший курс школьной математики
Кратчайший курс школьной математики .
. 1.5.4. Деление дробей
1.5.4. Деление дробей 1.5.2. Как перевести десятичную дробь в обыкновенную?
1.5.2. Как перевести десятичную дробь в обыкновенную?