5.4. Периодичность и взаимосвязь функций.
Формулы приведения
На это уже все обратили внимание. Если к ЛЮБОМУ углу 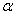 прибавить или вычесть прибавить или вычесть 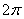 , то получится то же самое значение синуса и косинуса: , то получится то же самое значение синуса и косинуса:
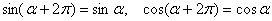 – по причине периодичности этих функций. И, кроме того, синус и косинус можно взаимно превращать друг в друга, «сдвигая» аргумент на – по причине периодичности этих функций. И, кроме того, синус и косинус можно взаимно превращать друг в друга, «сдвигая» аргумент на 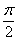 , например: , например: 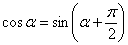 . Желающие могут построить график функции . Желающие могут построить график функции 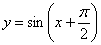 и убедиться в том, что это не что иное, как график и убедиться в том, что это не что иное, как график 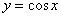 . .
Кстати, почему для общих объяснений я использую букву «альфа»? А дело в том, что «альфа» может быть не только переменной
«икс», но и сложной функцией, например: 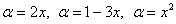 или ещё более сложной. или ещё более сложной.
Аналогично, в силу периодичности тангенса и котангенса:
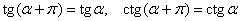 и, кроме того, эти функции тоже могут
превращаться друг в друга, в частности: и, кроме того, эти функции тоже могут
превращаться друг в друга, в частности: 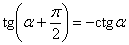 . .
Таким образом, если к углу прибавлены (или вычтены) значения 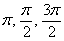 , ,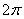 , то мы можем избавиться от этих «добавок». Для этого используют так называемые
формулы приведения, которые вы можете найти в Приложении Тригонометрические таблицы, и некоторые из которых я только что
привёл выше. Существуют формальные правила, по которым осуществляются превращения, и желающие могут отыскать этот материал в школьном курсе
математики. , то мы можем избавиться от этих «добавок». Для этого используют так называемые
формулы приведения, которые вы можете найти в Приложении Тригонометрические таблицы, и некоторые из которых я только что
привёл выше. Существуют формальные правила, по которым осуществляются превращения, и желающие могут отыскать этот материал в школьном курсе
математики.
Иногда формулы приведения используют не для упрощения, а для того, чтобы наоборот – усложнить запись, например, записать 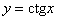 в виде в виде 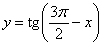 с целью дальнейших преобразований или анализа этой функции. с целью дальнейших преобразований или анализа этой функции.
Разумеется, эти принципы справедливы и для бОльшего количества периодов, например: 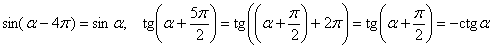 и т.д. и т.д.
Продолжаем изучать преобразования, позволяющие упростить жизнь:
 5.5. Распространённые тригонометрические формулы 5.5. Распространённые тригонометрические формулы
 5.3. Тригонометрические функции 5.3. Тригонометрические функции
| Оглавление |
|