|
Ваш репетитор, справочник и друг!
|
5.5. Распространённые тригонометрические формулыСледующие несколько фактов и формул нужно просто запомнить наизусть! Без них ваша учёба может закончиться самым скверным образом. Во-первых, на практике очень часто используют нечётность синуса и чётность косинуса, а именно, выносят «минус» из-под синуса: Осуществимы и обратные действия – «минус» можно «затолкать» под синус: Особо подчёркиваю, что здесь мы не получаем каких-то новых функций! Эти преобразования равносильны. В частности, Ещё одна ходовая вещь, которую нужно запомнить «намертво» – это основное тригонометрическое тождество:
Аргумент Чуть позже мы выведем из этого тождества ещё несколько полезных формул. Внимательные читатели ещё в прошлой главе подметили, что тангенс и котангенс – это два взаимно
обратных отношения: Теперь немного расслабьтесь, поскольку критически важные формулы позади, и вы спасены :) Вся прелесть математики состоит в том, что знать нужно
немного, и из этого немного можно вывести очень много! Иногда даже маленькую Вселенную. Получим несколько полезных формул из основного
тригонометрического тождества. Прежде всего, здесь напрашивается выразить синус через косинус и наоборот: Если тождество разделить почленно на Думал не говорить, но всё-таки скажу: не путайте записи И ещё раз заостряю внимание, что параметр «альфа» может быть не только буковкой «икс», но и сложной функцией! Все формулы
работают: Следующая группа – это формулы двойного угла: Примеры использования: Мегапопулярные формулы понижения степени: Запоминать их не нужно, сами запомнятся :). Натыкаться будете на каждом шагу. Примеры: Разумеется, все рассматриваемые формулы работают и в обратном направлении, так, степень иногда требуется и повысить: Ну и еще куча похожих друг на друга формул. Сразу скажу, что них есть одно замечательное свойство – упорно не запоминаться. Я сотни раз искал их в справочнике, так и не запомнилась ни одна. Итак, для произвольных углов «альфа» и «бета» справедливо следующее. Раз:
Два: Три: Есть еще аналогичные формулы для тангенсов и котангенсов, но о них не будем, в 99,9% случаях – не встретите. Да и перечисленные формулы
встречаются довольно редко. Но встречаются. Поэтому примеры употребления (1-я формула из каждой группы):
|
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Кратчайший курс школьной математики
Кратчайший курс школьной математики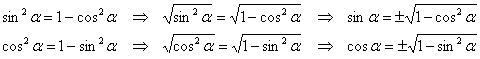
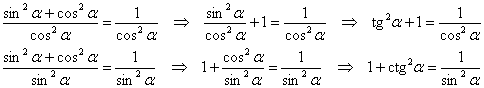
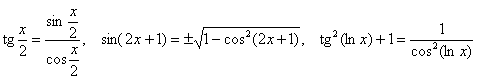 и так далее.
и так далее.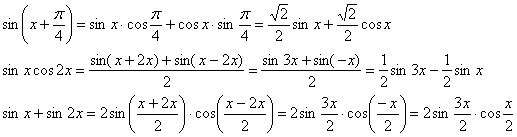
 5.6. Обратные тригонометрические функции
5.6. Обратные тригонометрические функции 5.4. Периодичность и взаимосвязь функций. Формулы приведения
5.4. Периодичность и взаимосвязь функций. Формулы приведения