5.3. Тригонометрические функции
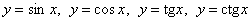 , где угол , где угол 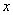 выражен в радианах (!). выражен в радианах (!).
Данные функции каждому действительному углу 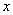 ставят в соответствие его синус, косинус, тангенс и котангенс (если они
существуют). ставят в соответствие его синус, косинус, тангенс и котангенс (если они
существуют).
По указанной выше причине тригонометрические функции периодичны. Геометрически это выражается тем, что у графика бесконечно повторяется один и
тот же кусок. Рассмотрим наших пациентов по порядку:
График функции 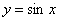 называется синусоидой: называется синусоидой:
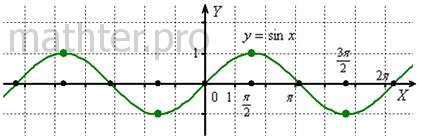
Данная функция является периодической с периодом 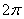 . Выберем любой промежуток длиной «два пи», проще всего посмотреть на
отрезок . Выберем любой промежуток длиной «два пи», проще всего посмотреть на
отрезок 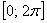 . …Взглянули? Легко понять, что этот кусок
графика бесконечно «тиражируется» влево и вправо. Кроме того, синус нечётен: . …Взглянули? Легко понять, что этот кусок
графика бесконечно «тиражируется» влево и вправо. Кроме того, синус нечётен: 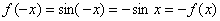 и синусоида симметрична относительно начала координат. и синусоида симметрична относительно начала координат.
График 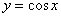 представляет собой синусоиду,
сдвинутую на представляет собой синусоиду,
сдвинутую на 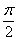 влево: влево:
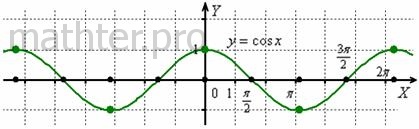
Данная функция тоже периодическая (с тем же периодом), однако является чётной:
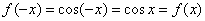 , и её график симметричен относительно оси , и её график симметричен относительно оси 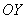 . .
Синус и косинус ограничены и могут принимать значения лишь из отрезка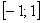 : :
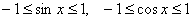
Тангенс 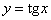 (слева) и котангенс (слева) и котангенс 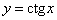 тоже как братья: тоже как братья:
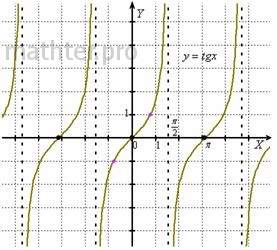 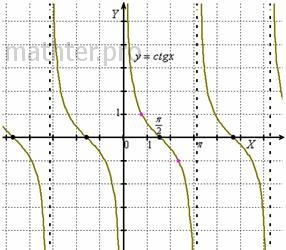
И если синус с косинусом непрерывны на всей числовой прямой, то здесь графики терпят разрывы. А именно, тангенс не
определён в точках 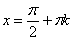 , где , где 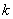 принимает все целые значения, а котангенса не
существует в точках принимает все целые значения, а котангенса не
существует в точках 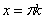 . Через эти точки проходят вертикальные асимптоты графиков (пунктирные линии). . Через эти точки проходят вертикальные асимптоты графиков (пунктирные линии).
Легко видеть, что обе функции периодичны, но период у них меньше, чем у синуса с косинусом, и составляет 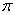 радиан (т.е. через каждые радиан (т.е. через каждые 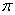 график повторяется). При этом тангенс нечётный: график повторяется). При этом тангенс нечётный: 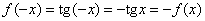 и его график симметричен относительно начала координат. С котангенсом та же история. и его график симметричен относительно начала координат. С котангенсом та же история.
При ручном построении графиков следует проявить аккуратность, так как 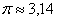 . Крайне не рекомендую «округлять» масштаб по оси . Крайне не рекомендую «округлять» масштаб по оси 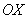 («пи» = 3 клетки), это весьма дурной тон. Помимо очевидных,
желательно использовать дополнительные опорные точки, в частности, значения («пи» = 3 клетки), это весьма дурной тон. Помимо очевидных,
желательно использовать дополнительные опорные точки, в частности, значения 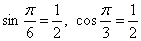 , а для тангенсов и котангенсов точки: , а для тангенсов и котангенсов точки: 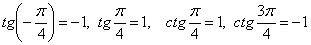 (см. чертежи выше). (см. чертежи выше).
 5.4. Периодичность и взаимосвязь функций. Формулы приведения 5.4. Периодичность и взаимосвязь функций. Формулы приведения
 5.2. Определение синуса, косинуса, тангенса через единичную окружность 5.2. Определение синуса, косинуса, тангенса через единичную окружность
| Оглавление |
|

 Кратчайший курс школьной математики
Кратчайший курс школьной математики



 5.4. Периодичность и взаимосвязь функций. Формулы приведения
5.4. Периодичность и взаимосвязь функций. Формулы приведения 5.2. Определение синуса, косинуса, тангенса через единичную окружность
5.2. Определение синуса, косинуса, тангенса через единичную окружность