5.2. Определение синуса, косинуса,
тангенса и котангенса через единичную окружность
Не так давно мы определили эти отношения для острого угла, и
сейчас распространим на произвольный угол. Для этого используют так называемую единичную окружность (радиуса 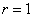 ). Изобразим её в декартовой системе с центром в начале
координат: ). Изобразим её в декартовой системе с центром в начале
координат:
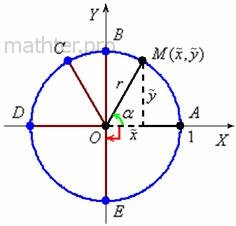 Рассмотрим
произвольную точку Рассмотрим
произвольную точку 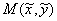 , принадлежащую
окружности, и положительно ориентированный угол , принадлежащую
окружности, и положительно ориентированный угол 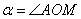 (зелёная стрелка). (зелёная стрелка).
Синусом угла 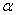 называют отношение
ординаты точки называют отношение
ординаты точки 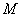 к радиусу окружности: к радиусу окружности: 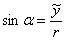 . .
Косинусом угла 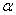 называют отношение
абсциссы точки называют отношение
абсциссы точки 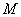 к радиусу окружности: к радиусу окружности:
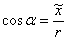 . .
Тангенс угла 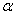 – есть отношение – есть отношение 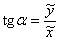 (если (если 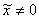 ), и котангенс: ), и котангенс: 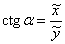 (если (если 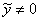 ). ).
Так, углам 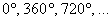 (да-да, угол
можно «накручивать» и дальше!) соответствуют точка (да-да, угол
можно «накручивать» и дальше!) соответствуют точка 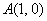 , и поэтому: , и поэтому: 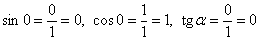 , а котангенса не существует, ибо ордината этой точки равна нулю. , а котангенса не существует, ибо ордината этой точки равна нулю.
Углу 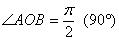 соответствует точка соответствует точка 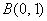 , следовательно: , следовательно:
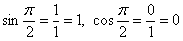 , тангенса не существует, , тангенса не существует, 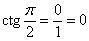 . .
Углу 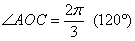 соответствует точка соответствует точка 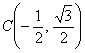 , следовательно: , следовательно:
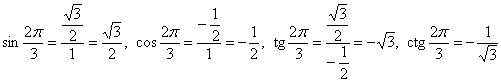
Угол 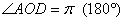 – самостоятельно
(сверьтесь по Тригономометрической таблице). – самостоятельно
(сверьтесь по Тригономометрической таблице).
Аналогично для отрицательно ориентированных углов. В частности, углу 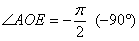 (красная стрелка на
чертеже), соответствует точка (красная стрелка на
чертеже), соответствует точка 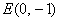 , следовательно: , следовательно: 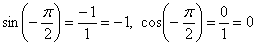 , тангенс аминь, , тангенс аминь, 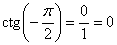 . .
На практике бывает удобно как «прикрутить» оборот к углу, так и «скрутить лишние». Так, угла 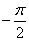 нет в Тригонометрической таблице, но к нему можно мысленно
прибавить нет в Тригонометрической таблице, но к нему можно мысленно
прибавить 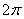 (один оборот), в результате чего
получится угол в (один оборот), в результате чего
получится угол в 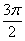 радиан с теми же самыми
значениями синуса, косинуса и котангенса. И, наоборот, в некоторых задачах появляются углы с «лишними» оборотами. Рассмотрим, например,
угол радиан с теми же самыми
значениями синуса, косинуса и котангенса. И, наоборот, в некоторых задачах появляются углы с «лишними» оборотами. Рассмотрим, например,
угол 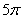 – здесь целесообразно «скрутить» два оборота: – здесь целесообразно «скрутить» два оборота: 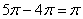 , получая эквивалентный угол. , получая эквивалентный угол.
И, как вы правильно догадались, угол можно «накручивать» до бесконечности в любом направлении. Представьте, что по единичной окружности «ездит»
точка. По мере того, как мы будем проходить оборот за оборотом (в любую сторону) значения синусов и компании будут периодически
повторяться. Таким образом, возникают:
 5.3. Тригонометрические функции 5.3. Тригонометрические функции
 5.1. Об угле подробно 5.1. Об угле подробно
| Оглавление |
|