|
Ваш репетитор, справочник и друг!
|
4.2. ТреугольникиОглавление: Понятие треугольника Понятие треугольникаТреугольник – это геометрическая фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, соединяющих эти точки. Треугольник стандартно обозначают значком Медиана – это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Например, Справка: отрезки равной длины обозначают одинаковыми засечками, а равные углы – одинаковыми дугами. Длину отрезка обозначают знаком модуля. Биссектриса – это луч, исходящий из вершины угла и делящий этот угол на два равных угла.
Например, В общем случае точки пересечения высот, медиан и биссектрис не совпадают. И, наверное, вам не нужно объяснять понятие площади (вспоминаем, квадратные метры, дачные «сотки» и т.д.). Площадь
треугольника равна половине произведения длины стороны (любой) на длину опущенной к ней высоты, в частности: Повторим частные случаи треугольников и их основные свойства: Равнобедренный треугольникТреугольник, у которого две стороны равны, называется равнобедренным. Равные стороны ( Равносторонний треугольникТреугольник, у которого все стороны равны, называется равносторонним. Равносторонний треугольник также называют правильным треугольником. Прямоугольный треугольник и теорема ПифагораТреугольник с прямым углом называется прямоугольным. Сторона, лежащая напротив прямого угла, является самой длинной и называется гипотенузой Теорема Пифагора: сумма квадратов длин катетов равна квадрату длины гипотенузы: Так, если известны катеты Справка: если в метрических (вычислительных) задачах не задана размерность (сантиметры, метры, литры, бараны и т.д.), то хорошим тоном считается указывать единицы, сокращённо: ед. И наоборот, если известна гипотенуза Синус, косинус, тангенс и котангенс острого углаГоворя простым языком, это пропорции (соотношения) между сторонами прямоугольного треугольника, зависящие от его острых
углов. Нагляднее сразу рассмотреть конкретный треугольник, например, египетский – со сторонами 3, 4 и 5 ед.: А теперь мякотка: синус, косинус тангенс и котангенс не зависят от размеров треугольника. Они зависят только от значения
острого угла. Так, Значения синусов, косинусов, тангенсов / котангенсов находят с помощью специальной таблицы (см. Приложение Тригонометрические таблицы) либо с помощью калькулятора. Следует отметить, что в тригонометрии перечисленные отношения определяются функциями – для произвольного угла, не только острого. Подобные треугольники
Соответствующие стороны подобных треугольников пропорциональны: Коэффициент Разумеется, подобными могут быть не только прямоугольные, и не только треугольники, а вообще произвольные геометрические фигуры. Например, матрёшки с одинаковой росписью. Если мы возьмём самую маленькую матрёшку, то её пропорции будут точно такими же, как и у всех остальных матрёшек, как и у самой большой.
|
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Кратчайший курс школьной математики
Кратчайший курс школьной математики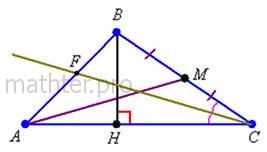 Высота – это перпендикуляр, опущенный из
вершины треугольника на противоположную сторону (или её продолжение). Например,
Высота – это перпендикуляр, опущенный из
вершины треугольника на противоположную сторону (или её продолжение). Например, 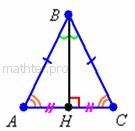
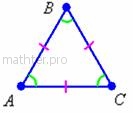 Все углы этого треугольника тоже равны и каждый из них
равен 60° (
Все углы этого треугольника тоже равны и каждый из них
равен 60° (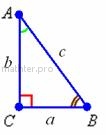 Нетрудно догадаться, что два других угла –
Нетрудно догадаться, что два других угла –  Далее для простоты изложения под стороной я буду
подразумевать её длину.
Далее для простоты изложения под стороной я буду
подразумевать её длину. 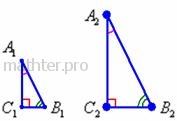 К этому понятию мы только что подошли. Треугольники
являются подобными, если их соответствующие углы (а значит, и их
К этому понятию мы только что подошли. Треугольники
являются подобными, если их соответствующие углы (а значит, и их  4.3. Четырехугольники
4.3. Четырехугольники 4.1. Геометрия. Элементарные геометрические фигуры
4.1. Геометрия. Элементарные геометрические фигуры