5.1. Об угле подробно
Тригонометрия изучает углы, тригонометрические функции (синус и компанию), формулы, уравнения, неравенства и иже с ними. Начнём с базового понятия – угла.
Во-первых, повторим определение, которое уже встретилось в курсе:) геометрии: угол – это геометрическая фигура, образованная двумя лучами, исходящими из одной точки. Заметьте, что эта конструкция задаёт два угла (зелёная и малиновая стрелки), но из контекста задач обычно понятно, о каком угле идёт речь:
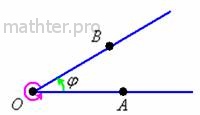 Обозначения: Обозначения: 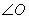 , , 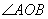 , маленькие греческие буквы , маленькие греческие буквы 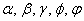 и др. Существуют и другие способы. и др. Существуют и другие способы.
Угол чаще отсчитывают против часовой стрелки, такой порядок называют положительным направлением отсчёта или положительной ориентацией угла.
«Открутку» угла можно провести и в противоположном направлении – от луча 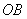 к лучу к лучу 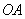 , в результате получится отрицательно ориентированный угол. К такому углу добавляется знак «минус», так, если , в результате получится отрицательно ориентированный угол. К такому углу добавляется знак «минус», так, если 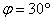 («фи»), то («фи»), то 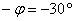 . Во многих задачах ориентация угла не имеет значения, и его принимают положительным. . Во многих задачах ориентация угла не имеет значения, и его принимают положительным.
Углы измеряют в градусах, радианах и более редких единицах. И если градусы представляет любой обыватель, то радианы не помнят даже некоторые «технари». Изобразим на чертеже окружность произвольного радиуса 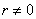 с центром в точке с центром в точке 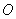 : :
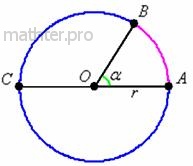 Радиан – это центральный угол Радиан – это центральный угол 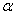 , такой, что длина соответствующей дуги , такой, что длина соответствующей дуги 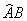 (малиновый цвет), равна радиусу (малиновый цвет), равна радиусу 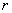 окружности. Радиан не зависит от конкретного значения окружности. Радиан не зависит от конкретного значения  и примерно равен и примерно равен 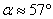 . .
Радианная мера угла – это отношение длины дуги 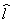 между сторонами угла к радиусу окружности: между сторонами угла к радиусу окружности: 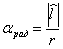 . .
Выясним, сколько радиан содержит, например, развёрнутый угол 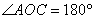 . Из известной формулы длины окружности . Из известной формулы длины окружности 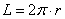 следует, что длина верхней полуокружности равна следует, что длина верхней полуокружности равна 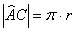 , таким образом, в 180 градусах содержится: , таким образом, в 180 градусах содержится: 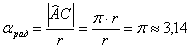 радиан. Полный оборот радиан. Полный оборот 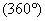 включает в себя включает в себя 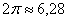 радиан (примерно 6,28 углов радиан (примерно 6,28 углов 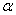 ). Да, углы мы измеряем… в углах! (радианах) ). Да, углы мы измеряем… в углах! (радианах)
Для перевода градусов в радианы удобно использовать формулу 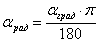 . Переведём в радианы, например, угол . Переведём в радианы, например, угол 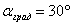 : : 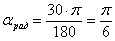 радиан. радиан.
Обратно, радианы переводятся в градусы по формуле: 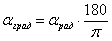 . Например, переведём в градусы . Например, переведём в градусы 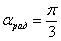 : : 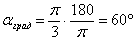 . .
В тригонометрии в ходу радианы.
Это, можно сказать, тригонометрическая практическая аксиома :) И поэтому если вам предложены градусы, то для дальнейших преобразований их почти всегда придётся перевести в радианы (формула выше). Теперь возвращаемся к знакомой теме:
 5.2. Определение синуса, косинуса, тангенса через единичную окружность 5.2. Определение синуса, косинуса, тангенса через единичную окружность
 4.5. Основные пространственные фигуры 4.5. Основные пространственные фигуры
| Оглавление |
|

 Кратчайший курс школьной математики
Кратчайший курс школьной математики Обозначения:
Обозначения:  Радиан – это
Радиан – это  5.2. Определение синуса, косинуса, тангенса через единичную окружность
5.2. Определение синуса, косинуса, тангенса через единичную окружность 4.5. Основные пространственные фигуры
4.5. Основные пространственные фигуры