4.5. Основные пространственные фигуры
Во-первых, плоскость, которая сама по себе является одной из элементарных геометрических
фигур. На чертеже плоскость чаще всего изображают параллелограммом, что создаёт впечатление пространства:
 Плоскость бесконечна, и у нас есть возможность
изобразить лишь её кусочек. На практике помимо параллелограмма также прорисовывают овал или даже облачко. Плоскость бесконечна, и у нас есть возможность
изобразить лишь её кусочек. На практике помимо параллелограмма также прорисовывают овал или даже облачко.
Реальные плоскости, которые встречаются в практических задачах, могут располагаться как угодно – мысленно возьмите чертёж в руки и покрутите его
в пространстве, придав плоскости любой наклон, любой угол
Обозначения: плоскости принято обозначать маленькими греческими буквами 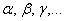 .
На чертеже плоскость отмечена буквой .
На чертеже плоскость отмечена буквой 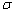 («сигма»). («сигма»).
Призма – это фигура, состоящая из двух одинаковых многоугольников (оснований), лежащих в параллельных плоскостях, и боковых сторон,
которые представляют собой параллелограммы. На чертеже ниже изображена треугольная призма:
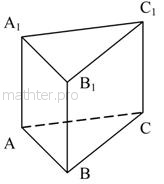 Основаниями данной призмы являются равные треугольники Основаниями данной призмы являются равные треугольники 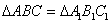 , а боковыми сторонами – прямоугольники , а боковыми сторонами – прямоугольники 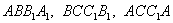 . Любую сторону призмы также
называют гранью, а любой отрезок – ребром. . Любую сторону призмы также
называют гранью, а любой отрезок – ребром.
Линии, которые мы не видим, принято проводить пунктиром! В данном случае от нас спряталось ребро 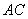 . .
Разумеется, треугольники не обязаны располагаться строго друг над другом, поэтому в общем случае у нас получится «косая» призма. Здесь же
боковые рёбра перпендикулярны основаниями, и, очевидно, объём этой призмы равен: 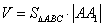 . .
Если основаниями призмы являются не треугольники, а параллелограммы, то получится (не сломать бы язык) параллелепипед. В
качестве примера приведу популярнейший частный случай – прямоугольный параллелепипед:
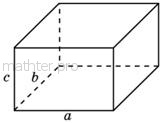 Все грани этого «пипеда» – прямоугольники, причём
противоположные грани параллельны и равны, а углы между смежными рёбрами составляют Все грани этого «пипеда» – прямоугольники, причём
противоположные грани параллельны и равны, а углы между смежными рёбрами составляют 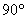 . .
Эта форма встречается повсеместно (спичечный коробок, чемодан, комната и т.д.). Очевидно, что объём «пипеда» равен произведению длин трёх
смежных сторон: 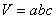 . .
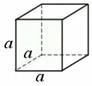 Если все рёбра равны, то получается куб объёма Если все рёбра равны, то получается куб объёма
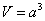 , объём, кстати, и измеряют «кубиками». Но литры, конечно,
удобнее. , объём, кстати, и измеряют «кубиками». Но литры, конечно,
удобнее.
И на всякий пожарный: не путайте объём с массой! Литровая банка ртути намного тяжелее литровой банки воды (хотя объём одинаков). Впрочем, это
уже из кратчайшего курса физики :).
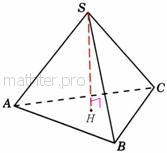 Пирамида – это многогранник, одна грань которого
(основание) произвольный многоугольник, а остальные грани (боковые стороны) – треугольники с общей вершиной. Так, в основании египетских пирамид
лежат прямоугольники…, представили? Отлично! Пирамида – это многогранник, одна грань которого
(основание) произвольный многоугольник, а остальные грани (боковые стороны) – треугольники с общей вершиной. Так, в основании египетских пирамид
лежат прямоугольники…, представили? Отлично!
Пирамида с основанием-треугольником называется треугольной пирамидой или тетраэдром. На рисунке слева точка 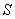 является вершиной, а является вершиной, а 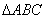 – основанием пирамиды. – основанием пирамиды.
Объём пирамиды (любой) можно вычислить по формуле 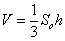 , где , где 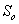 – площадь основания, – площадь основания, 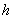 – длина проведённой к
нему высоты, для нашего тетраэдра: – длина проведённой к
нему высоты, для нашего тетраэдра: 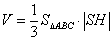 . .
Сфера – это множество точек пространства, равноудалённых от заданной точки 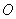 : :
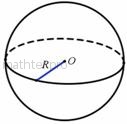 Точка Точка 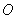 называется центром сферы, а значение называется центром сферы, а значение 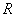 – радиусом. Площадь поверхности сферы равна: – радиусом. Площадь поверхности сферы равна: 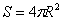 . .
Тело, ограниченное сферой (+ сама сфера), называется шаром. Не путайте эти понятия! Сфера – поверхность, шар – тело.
Объём шара (!) можно вычислить по формуле 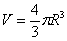 . .
Следующие тела и поверхности я приведу в описательном порядке (без строгих определений). Всем знакомый прямой круговой цилиндр:
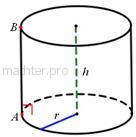 Данное тело ограничено равными параллельными кругами сверху и снизу (основания цилиндра), а боковая поверхность порождена образующими (в частности, Данное тело ограничено равными параллельными кругами сверху и снизу (основания цилиндра), а боковая поверхность порождена образующими (в частности, 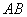 ) – перпендикулярами, которые соединяют окружности. Площадь боковой
поверхности: ) – перпендикулярами, которые соединяют окружности. Площадь боковой
поверхности: 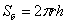 , где , где 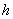 – высота цилиндра, а – высота цилиндра, а 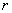 – радиус
основания. Чтобы найти площадь поверхности всего цилиндра нужно приплюсовать площадь двух кругов: – радиус
основания. Чтобы найти площадь поверхности всего цилиндра нужно приплюсовать площадь двух кругов: 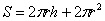 . Объём цилиндра: . Объём цилиндра: 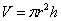 . .
Существует великое множество других цилиндров, но во избежание путаницы мы ограничимся лишь этим частным случаем, рАвно, как и одним частными
случаем конуса:
Прямой круговой конус – это тело, ограниченное кругом (основание конуса) и образующими – отрезками равной длины 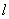 , которые соединяют окружность с вершиной конуса , которые соединяют окружность с вершиной конуса 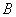 , которая расположена строго над (или под) центром , которая расположена строго над (или под) центром 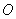 круга: круга:
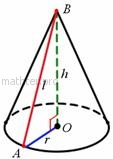 Если известен радиус основания Если известен радиус основания 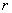 и высота конуса и высота конуса 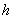 , то длину образующей можно найти с помощью теоремы
Пифагора по формуле , то длину образующей можно найти с помощью теоремы
Пифагора по формуле 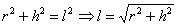 . Площадь боковой поверхности конуса равна: . Площадь боковой поверхности конуса равна: 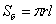 , а чтобы вычислить площадь поверхности всего конуса нужно добавить площадь
круга: , а чтобы вычислить площадь поверхности всего конуса нужно добавить площадь
круга: 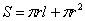 . .
И объём конуса: 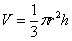 . Есть ещё усечённый конус, но… . Есть ещё усечённый конус, но…
Информации этой главы должно хватить в 90-95% случаев! Ну а для случаев других есть учебники / справочники, где можно
отыскать более редкие фигуры и формулы.
…никогда не думал, что прикладную геометрию можно изложить на 9,5 страницах… :)
 5.1. И немного тригонометрии 5.1. И немного тригонометрии
 4.4. Окружность и круг 4.4. Окружность и круг
| Оглавление |
|

 Кратчайший курс школьной математики
Кратчайший курс школьной математики Плоскость бесконечна, и у нас есть возможность
изобразить лишь её кусочек. На практике помимо параллелограмма также прорисовывают овал или даже облачко.
Плоскость бесконечна, и у нас есть возможность
изобразить лишь её кусочек. На практике помимо параллелограмма также прорисовывают овал или даже облачко.  Основаниями данной призмы являются равные
Основаниями данной призмы являются равные  Все грани этого «пипеда» – прямоугольники, причём
противоположные грани параллельны и равны, а углы между смежными рёбрами составляют
Все грани этого «пипеда» – прямоугольники, причём
противоположные грани параллельны и равны, а углы между смежными рёбрами составляют  Если все рёбра равны, то получается куб объёма
Если все рёбра равны, то получается куб объёма
 Пирамида – это многогранник, одна грань которого
(основание) произвольный многоугольник, а остальные грани (боковые стороны) – треугольники с общей вершиной. Так, в основании египетских пирамид
лежат прямоугольники…, представили? Отлично!
Пирамида – это многогранник, одна грань которого
(основание) произвольный многоугольник, а остальные грани (боковые стороны) – треугольники с общей вершиной. Так, в основании египетских пирамид
лежат прямоугольники…, представили? Отлично! Точка
Точка  Данное тело ограничено равными параллельными
Данное тело ограничено равными параллельными  Если известен радиус основания
Если известен радиус основания  5.1. И немного тригонометрии
5.1. И немного тригонометрии 4.4. Окружность и круг
4.4. Окружность и круг