|
Ваш репетитор, справочник и друг!
|
4.4. Окружность и круг
Отрезок, соединяющий центр с любой точкой окружности Длина окружности равна: Отрезок, соединяющий две точки окружности, называется хордой (например, Окружность не следует путать с кругом. Круг – это множество точек лежащих внутри окружности + сама окружность. Формула
площади круга: И для закрепления материала ОБЯЗАТЕЛЬНО прорешиваем следующие задачки: Задание 9 а) Найти высоту Задачи по геометрии (да и не только) удобно снабжать схематическими чертежами Это облегчает решение. Поэтому если задача не самая простая, то не стесняйтесь: б) Известен угол в) Что можно сказать о г) Найти площадь параллелограмма д) Найти диагональ, площадь и периметр е) Найти площадь круга, если известна длина Решения и ответы в конце книги. Как вы помните, весь курс школьной геометрии делится на два больших раздела: геометрия плоскости (планиметрия) и геометрия пространства (стереометрия). Перечисленные выше фигуры можно рассматривать как на плоскости, так и в трёхмерном пространстве, ну а сейчас пришло время кратко повторить именно 3D-объекты:
|
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Кратчайший курс школьной математики
Кратчайший курс школьной математики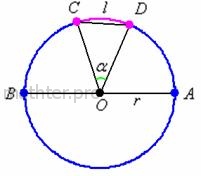 Окружность – это множество точек, равноудалённых от
фиксированной точки
Окружность – это множество точек, равноудалённых от
фиксированной точки  4.5. Основные пространственные фигуры
4.5. Основные пространственные фигуры 4.3. Четырехугольники
4.3. Четырехугольники