5.8. Тригонометрические неравенства
Только что мы разобрали уравнения 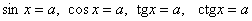 и сейчас очередь за соответствующими неравенствами – строгими и сейчас очередь за соответствующими неравенствами – строгими 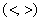 и нестрогими и нестрогими 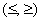 . Эти неравенства тоже можно решить разными способами, но я по-прежнему ратую за графический метод решения, он полезнее и нагляднее. Вспоминаем общий принцип: . Эти неравенства тоже можно решить разными способами, но я по-прежнему ратую за графический метод решения, он полезнее и нагляднее. Вспоминаем общий принцип:
Решением неравенства 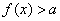 являются те интервалы числовой прямой (оси являются те интервалы числовой прямой (оси 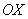 ), на
которых график функции ), на
которых график функции 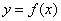 расположен выше графика прямой расположен выше графика прямой 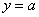 . И, наоборот, неравенству . И, наоборот, неравенству 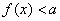 соответствуют
интервалы, где график соответствуют
интервалы, где график 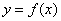 ниже графика ниже графика 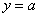 . Если неравенства нестрогие,
то к решению нужно добавить допустимые граничные точки, то есть вместо интервалов получатся отрезки либо полуинтервалы. . Если неравенства нестрогие,
то к решению нужно добавить допустимые граничные точки, то есть вместо интервалов получатся отрезки либо полуинтервалы.
И из этих соображений сразу «щёлкаются» некоторые примеры:
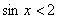 – решением этого неравенства являются все
значения «икс», поскольку синусоида – решением этого неравенства являются все
значения «икс», поскольку синусоида 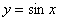 полностью лежит под графиком прямой полностью лежит под графиком прямой 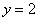 . Соответственно, неравенство . Соответственно, неравенство 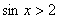 решений не имеет, т.к. выше прямой синусоиды нет. решений не имеет, т.к. выше прямой синусоиды нет.
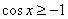 – решением этого неравенства тоже является любое
«икс»: – решением этого неравенства тоже является любое
«икс»: 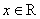 , ибо график , ибо график 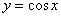 расположен не ниже прямой расположен не ниже прямой 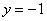 . .
Теперь переходим к общему случаю. В предыдущем параграфе я начал с синуса, и сейчас для разнообразия «запилим» с косинуса.
Алгоритм решения рассмотрим на конкретном примере: 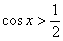 .
Решением данного неравенства являются те участки оси .
Решением данного неравенства являются те участки оси 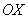 , на которых график , на которых график 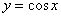 выше графика выше графика 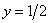 : :
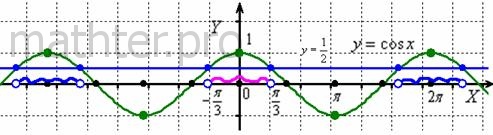
На картинке всё тип-топ, но как получить это красивое решение аналитически? Сначала нужно решить соответствующее уравнение: 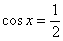 , по общей
формуле: , по общей
формуле: 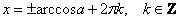 , при этом нас будут
интересовать два корня, которые расположены близко к началу координат. Очевидно, это корни , при этом нас будут
интересовать два корня, которые расположены близко к началу координат. Очевидно, это корни 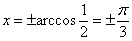 . Таким образом, неравенство . Таким образом, неравенство 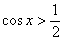 выполнено на интервале выполнено на интервале 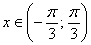 (малиновая штриховка) и из чертежа следует, что эта ситуация
повторяется через каждые (малиновая штриховка) и из чертежа следует, что эта ситуация
повторяется через каждые 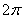 радиан, то
есть решением данного неравенства является множество интервалов: радиан, то
есть решением данного неравенства является множество интервалов:
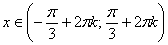 , где , где 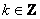 …. Громоздко, но довольно просто! Так, при …. Громоздко, но довольно просто! Так, при 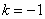 получаем интервал, который левее: получаем интервал, который левее: 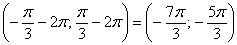 , а при , а при 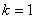 – интервал, который правее: – интервал, который правее: 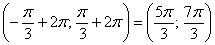 (синие штриховки). (синие штриховки).
Противоположному неравенству 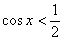 соответствуют
те участки оси соответствуют
те участки оси 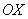 , на которых график косинуса ниже прямой. Нетрудно выяснить, что это интервал , на которых график косинуса ниже прямой. Нетрудно выяснить, что это интервал 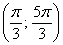 и его «клоны», повторяющиеся через каждые и его «клоны», повторяющиеся через каждые 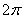 радиан: радиан: 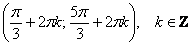 . .
Если аргумент тригонометрической функции более сложный, например, 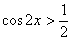 то неравенство удобно решить аналитически, используя некоторые геометрические факты и тот
же алгоритм. График функции то неравенство удобно решить аналитически, используя некоторые геометрические факты и тот
же алгоритм. График функции 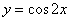 имеет такой же вид,
как и имеет такой же вид,
как и 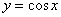 , только он сжат по горизонтали (как
«гармошка») в два раза. Сначала решим соответствующее уравнение: , только он сжат по горизонтали (как
«гармошка») в два раза. Сначала решим соответствующее уравнение: 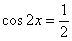 . По общей формуле: . По общей формуле: 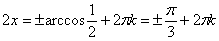 , откуда выражаем , откуда выражаем 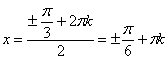 . Нас по-прежнему интересует два ближайших к нулю угла, и это углы . Нас по-прежнему интересует два ближайших к нулю угла, и это углы 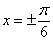 . На интервале . На интервале 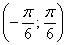 график график 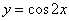 расположен выше прямой расположен выше прямой 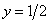 и эта ситуация повторяется через каждые (внимание!) и эта ситуация повторяется через каждые (внимание!) 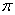 радиан (так как период сократился в 2 раза), таким образом, решение: радиан (так как период сократился в 2 раза), таким образом, решение: 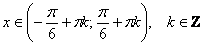 . .
И обещанный вывод формулы, выражающей косинус через синус на примере простого аргумента
(«икс»). Из основного тригонометрического тождества выражаем 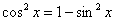 , после чего извлекли корень из обеих частей: , после чего извлекли корень из обеих частей: 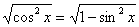 . Теперь вспоминаем, как извлекается этот
корень: . Теперь вспоминаем, как извлекается этот
корень: 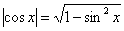 и как раскрывается модуль: и как раскрывается модуль: 
Решим неравенство 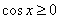 . График косинуса не
ниже прямой . График косинуса не
ниже прямой 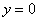 (оси (оси 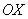 ) на отрезке ) на отрезке 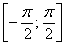 и аналогичная ситуация повторяется через каждые и аналогичная ситуация повторяется через каждые 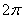 радиан. Таким образом, если радиан. Таким образом, если 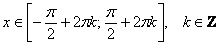 , то , то 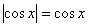 , и мы получаем формулу со знаком «плюс»: , и мы получаем формулу со знаком «плюс»: 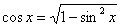 . Неравенство . Неравенство 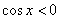 , очевидно, выполнено на интервалах , очевидно, выполнено на интервалах 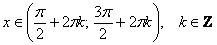 (анализируем чертёж выше), в этом случае мы получаем (анализируем чертёж выше), в этом случае мы получаем 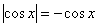 и формулу со знаком «минус»: и формулу со знаком «минус»: 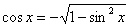
Аналогично с «зеркальной» формулой: 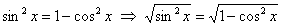 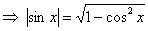 . Синусоида (представили в уме!) не ниже оси . Синусоида (представили в уме!) не ниже оси 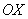 на отрезках на отрезках 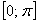 и иже с ним, поэтому при этих значениях угла: и иже с ним, поэтому при этих значениях угла: 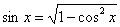 . Синусоида ниже оси . Синусоида ниже оси 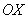 на интервалах на интервалах 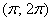 и иже с ним – при этих углах синус отрицателен, и в формуле следует поставить знак
«минус»: и иже с ним – при этих углах синус отрицателен, и в формуле следует поставить знак
«минус»: 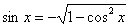
Таким образом, простые неравенства можно решать устно! – это доступно даже «чайнику», главное, помнить, как выглядят графики функций, и где они
пересекают ось абсцисс. Следует также заметить, что во многих задачах высшей математики неравенство нужно решить только
для одного (обычно первого) периода. Так, для неравенства 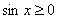 берут лишь отрезок берут лишь отрезок 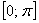 , а для , а для 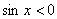 – лишь – лишь 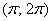 . .
И синусы (с тангенсами заодно) я очень скоро предложу вам для самостоятельного решения, после того, как мы разберём котангенс на примере
неравенства 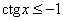 . .
Изобразим на чертеже график 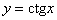 и прямой и прямой 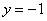 : :
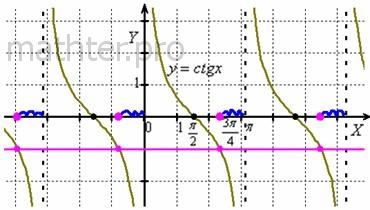 Нашему неравенству соответствуют те участки оси Нашему неравенству соответствуют те участки оси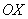 , где график
котангенса не выше прямой. Рассмотрим «главный» период котангенса (от 0 до «пи») и найдём «иксовую» координату
точки пересечения графиков: , где график
котангенса не выше прямой. Рассмотрим «главный» период котангенса (от 0 до «пи») и найдём «иксовую» координату
точки пересечения графиков: 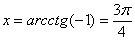 . Таким образом,
получаем полуинтервал . Таким образом,
получаем полуинтервал 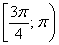 и, очевидно, эта ситуация
повторяется через каждые и, очевидно, эта ситуация
повторяется через каждые 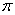 радиан: радиан: 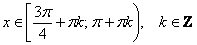
Легко понять, что противоположному неравенству 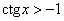 соответствует интервал соответствует интервал 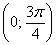 (где котангенс выше прямой) и его «клоны»: (где котангенс выше прямой) и его «клоны»: 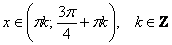 . Ну а неравенства . Ну а неравенства 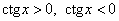 вообще решаются устно: вообще решаются устно: 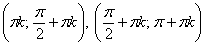 Если аргумент с множителем, например, Если аргумент с множителем, например, 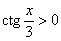 , то можно использовать тот же шаблон: , то можно использовать тот же шаблон: 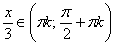 и для того, чтобы выразить «икс», нужно умножить на три каждую границу: и для того, чтобы выразить «икс», нужно умножить на три каждую границу: 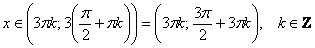 . График . График 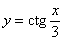 имеет такую же форму, как и имеет такую же форму, как и 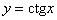 , но растянут по горизонтали в 3 раза (т.е. период был , но растянут по горизонтали в 3 раза (т.е. период был 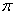 , а стал , а стал 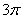 ). ).
И в заключение обещанный пункт для самостоятельного решения:
ж) Решить неравенства: 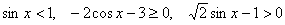 если если 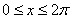 (найти решение на первом периоде), (найти решение на первом периоде), 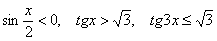 . .
Решения и ответы в конце книги.
И я Вас поздравляю с успешным (надеюсь) завершением курса!
Должен сказать, в нём есть что-то сакральное. Дело в том, что я получил советское образование и окончил 10 классов, и сейчас у меня получилось
ровно 100 страниц (по 10 на класс) и ровно 10 заданий для самостоятельного решения! Причём, и то, и другое вышло совершенно непреднамеренно – я
ничего не сокращал и ничего не «подгонял». Желаю успехов и до скорых встреч в курсе высшей математики!
 5.7. Простейшие тригонометрические уравнения 5.7. Простейшие тригонометрические уравнения
| Оглавление |
|

 Кратчайший курс школьной математики
Кратчайший курс школьной математики
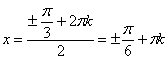 . Нас по-прежнему интересует два ближайших к нулю угла, и это углы
. Нас по-прежнему интересует два ближайших к нулю угла, и это углы  Нашему неравенству соответствуют те участки оси
Нашему неравенству соответствуют те участки оси 5.7. Простейшие тригонометрические уравнения
5.7. Простейшие тригонометрические уравнения