5.7. Простейшие тригонометрические уравнения
Нам будет достаточно повторить уравнения 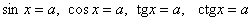 , где , где 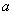 – константа. Ну и чуть более сложные, когда аргумент равен – константа. Ну и чуть более сложные, когда аргумент равен 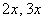 и т.п. В силу периодичности тригонометрических функций эти уравнения имеют бесконечно много решений, а синус с
косинусом могут не иметь их вовсе. И в самом деле, уравнению и т.п. В силу периодичности тригонометрических функций эти уравнения имеют бесконечно много решений, а синус с
косинусом могут не иметь их вовсе. И в самом деле, уравнению 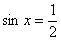 или или 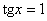 соответствует бесконечно много углов, а вот с соответствует бесконечно много углов, а вот с 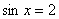 – печаль. – печаль.
С синуса и начнём: 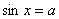 . Поскольку
синус ограничен, то это уравнение имеет корни только в том случае, если . Поскольку
синус ограничен, то это уравнение имеет корни только в том случае, если 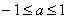 . .
И эти корни таковы, общая формула: 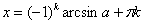 , где , где 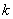 принимает все целые значения, сокращённо будем писать: принимает все целые значения, сокращённо будем писать: 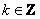 . .
Так решением уравнения 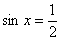 являются углы: являются углы:
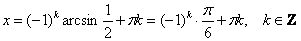
Распишем несколько штук для 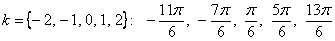
Довольно часто в задачах требуется найти какой-то конкретный угол (или углы), так, если по условию угол должен быть тупым, то следует выбрать корень 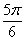 . .
А теперь важный вопрос: откуда взялась общая формула? В школьном курсе формулы выводятся с помощью единичной окружности, но сейчас нам гораздо полезнее вспомнить графический метод решения уравнений. Строим синусоиду 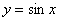 и прямую и прямую 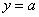 , например, , например, 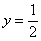 (малиновый цвет). После чего определяем «иксовые» координаты их точек
пересечения (малиновые отметки на оси (малиновый цвет). После чего определяем «иксовые» координаты их точек
пересечения (малиновые отметки на оси 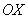 ): ):
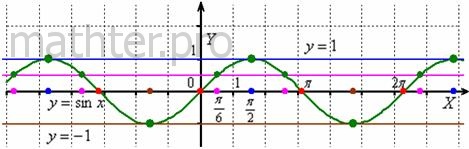
Это и есть корни. Осталось уловить периодичность расположения корней и сконструировать формулу. Отработаем этот принцип на важных частных случаях:
Решим графически уравнение 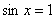 . Из чертежа следует,
что прямая . Из чертежа следует,
что прямая 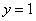 пересекает синусоиду пересекает синусоиду 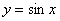 через каждые через каждые 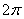 радиан, начиная от значения радиан, начиная от значения 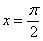 (выбираем самое маленькое). Таким образом, уравнение имеет корни (синие
точки): (выбираем самое маленькое). Таким образом, уравнение имеет корни (синие
точки):
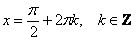 . Легко видеть, что решением уравнения . Легко видеть, что решением уравнения 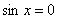 является множество углов является множество углов 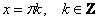 (красные точки), а решением (красные точки), а решением 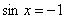 – углы – углы 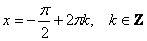 . .
Все формулы справедливы не только для переменной 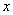 , но и для сложного аргумента, например, , но и для сложного аргумента, например, 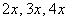 (самые популярные) и других. Решим, например, уравнение (самые популярные) и других. Решим, например, уравнение 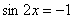 . Используем только что
выведенную частную формулу, только ВМЕСТО «икс» у нас «два икс»: . Используем только что
выведенную частную формулу, только ВМЕСТО «икс» у нас «два икс»: 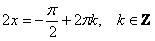 . Но это ещё не всё, ведь нам нужно выразить «икс»: . Но это ещё не всё, ведь нам нужно выразить «икс»: 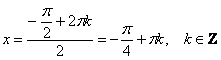 . .
Готово.
Разумеется, встречаются и «плохие» решения, рассмотрим уравнение 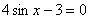 . Приведём его к виду . Приведём его к виду 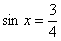 , и по общей формуле: , и по общей формуле: 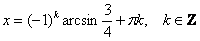 . Этот арксинус можно вычислить лишь приближенно: . Этот арксинус можно вычислить лишь приближенно: 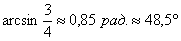 и поэтому ответ лучше оставить с арксинусом. и поэтому ответ лучше оставить с арксинусом.
Решим уравнение 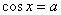 . Как и в случае с синусом, оно имеет корни, только если . Как и в случае с синусом, оно имеет корни, только если 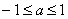 . Изобразим на чертеже графики функций . Изобразим на чертеже графики функций 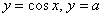 и определим «иксовые» координаты их точек пересечения. Во-первых,
обращаем внимание на самые близкие к нулю значения: и определим «иксовые» координаты их точек пересечения. Во-первых,
обращаем внимание на самые близкие к нулю значения: 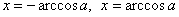 (красная и синяя точки вблизи нуля): (красная и синяя точки вблизи нуля):
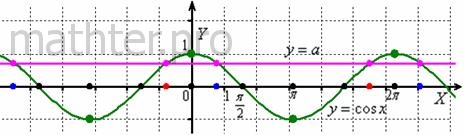
И анализируя точки пересечения графиков, легко понять, что «красные» корни повторяются через каждые 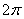 радиан: радиан: 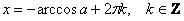 и «синие» корни тоже повторяются через этот же период: и «синие» корни тоже повторяются через этот же период: 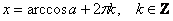 . Обе ветки решения можно объединить в общую формулу: . Обе ветки решения можно объединить в общую формулу: 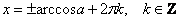
Решим, например, уравнение 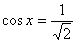 . Уловка здесь детская: избавляемся от иррациональности в знаменателе: . Уловка здесь детская: избавляемся от иррациональности в знаменателе: 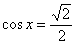 , после чего записываем «хороший» ответ: , после чего записываем «хороший» ответ:
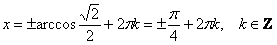 . Именно это случай я изобразил на схематическом
чертеже выше и желающие могут ещё раз осмыслить общую формулу, используя конкретные значения углов. . Именно это случай я изобразил на схематическом
чертеже выше и желающие могут ещё раз осмыслить общую формулу, используя конкретные значения углов.
И в качестве задания я предложу вам вывести три частные формулы для уравнений 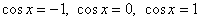 . Уже скоро на экранах ваших мониторов! :) Разумеется, аргумент может быть сложным: . Уже скоро на экранах ваших мониторов! :) Разумеется, аргумент может быть сложным: 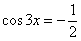 . Формула та же самая: . Формула та же самая: 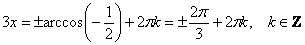 .
Единственное, не забываем выразить «икс», разделив всё семейство углов на три: .
Единственное, не забываем выразить «икс», разделив всё семейство углов на три: 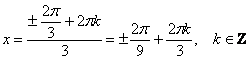 . .
Осталось два более простых уравнения.
Уравнение 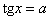 имеет решения при
любом значении имеет решения при
любом значении 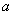 , и ситуация здесь прозрачна,
даже чертежа особо не нужно: «главная» ветка тангенса расположена на интервале , и ситуация здесь прозрачна,
даже чертежа особо не нужно: «главная» ветка тангенса расположена на интервале 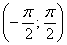 , берём отсюда угол: , берём отсюда угол: 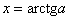 и добавляем периоды тангенса: и добавляем периоды тангенса:
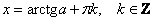 – общая формула. – общая формула.
В качестве примера решим приятное уравнение 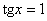 : :
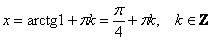 Готово! Готово!
И всё же приведу чертёж для этого и двух других частных случаев:
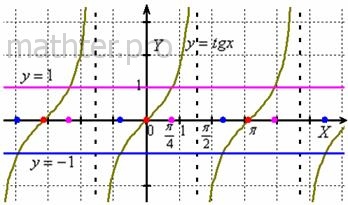 Решением уравнения Решением уравнения 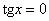 является множество углов является множество углов 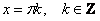 . .
Решением уравнения 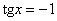 – множество: – множество:
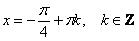
Эти формулы легко получить как аналитически (по общей формуле), так и графически.
Уравнение 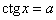 предлагаю для
самостоятельного изучения, в числе других заданий, которые уже нет сил – не могу не предложить: предлагаю для
самостоятельного изучения, в числе других заданий, которые уже нет сил – не могу не предложить:
Задание 10
а) Перевести из градусов в радианы или наоборот: 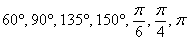 . .
б) Вычислить, не пользуясь калькулятором: 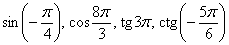 . .
в) Упростить: 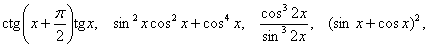
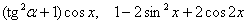 , , 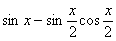 ; понизить степень до первой: ; понизить степень до первой:
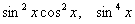 . .
г) Графическим методом решить уравнения 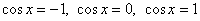 . .
д) Вывести (аналитически или графически) общую формулу для решения уравнения 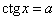 и получить частные формулы для и получить частные формулы для 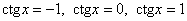 . .
е) Решить аналитически: 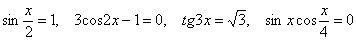 . .
Решения и ответы в конце книги, и ещё будет пункт ж) (в хорошем смысле :)), который я предложу вам после изучения следующего параграфа:
 5.8. Тригонометрические неравенства 5.8. Тригонометрические неравенства
 5.6. Обратные тригонометрические функции 5.6. Обратные тригонометрические функции
| Оглавление |
|

 Кратчайший курс школьной математики
Кратчайший курс школьной математики
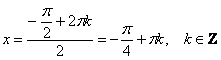 .
. 
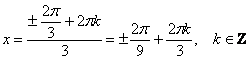 .
. Решением уравнения
Решением уравнения  5.8. Тригонометрические неравенства
5.8. Тригонометрические неравенства 5.6. Обратные тригонометрические функции
5.6. Обратные тригонометрические функции