5.6. Обратные тригонометрические функции
Оглашаю весь список: арксинус, арккосинус, арктангенс, арккотангенс. Они предназначены для того, чтобы по известному синусу, косинусу,
тангенсу или котангенсу угла, определить сам угол. Например, если 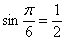 , то , то 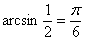 . Если . Если 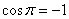 , то , то 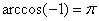 . Если . Если 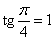 , то , то 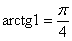 и и 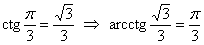 . .
Но здесь есть одна проблемка: дело в том, что значению 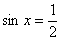 (например) соответствует бесконечно много углов, а обратная функция (как и любая функция) должна быть определена однозначно. И эта проблемка решена так,… объясню на конкретном
примере, а то у меня тут правило кошмарное получилось, которое я сразу удалил :). (например) соответствует бесконечно много углов, а обратная функция (как и любая функция) должна быть определена однозначно. И эта проблемка решена так,… объясню на конкретном
примере, а то у меня тут правило кошмарное получилось, которое я сразу удалил :).
Синус принимает все свои возможные значения (от –1 до 1) на отрезке 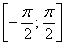 , и во избежание разночтений арксинус возвращает углы только из этого
отрезка: , и во избежание разночтений арксинус возвращает углы только из этого
отрезка:
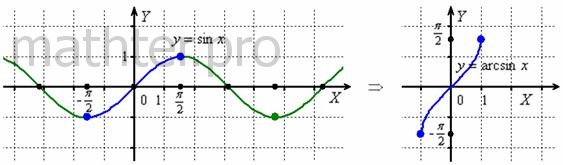
Так, если 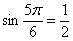 , то обратная функция все равно вернёт угол , то обратная функция все равно вернёт угол 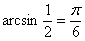 и уже к этому результату нужно «прикрутить» нужное количество
радиан и уже к этому результату нужно «прикрутить» нужное количество
радиан 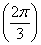 , чтобы получить , чтобы получить 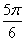 . Таким образом, функция . Таким образом, функция 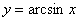 определена на отрезке определена на отрезке 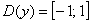
и, очевидно, нечётна, то есть, из-под арксинуса тоже можно вынести минус:
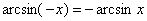
Аналогично, косинус принимает все свои возможные значения (от 1 до –1) на отрезке  , и поэтому арккосинус возвращает углы только из этого
промежутка: , и поэтому арккосинус возвращает углы только из этого
промежутка:
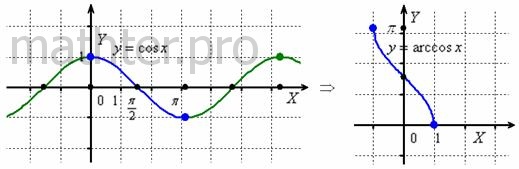
Функция 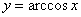 определена на том же промежутке определена на том же промежутке
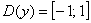 , однако не является чётной или нечётной. , однако не является чётной или нечётной.
С арктангенсом и арккотангенсом всё проще. График  представляет собой ветку тангенса, которая
«лежит на боку»: представляет собой ветку тангенса, которая
«лежит на боку»:
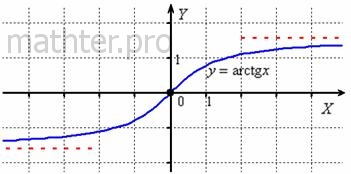
Данная функция определена на всей числовой прямой 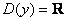 и возвращает углы из интервала и возвращает углы из интервала 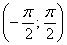 . Арктангенс нечётен: . Арктангенс нечётен: 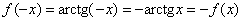 . График функции ограничен горизонтальными асимптотами . График функции ограничен горизонтальными асимптотами 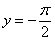 и и 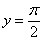 (красный пунктир). (красный пунктир).
График арккотангенса 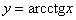 ограничен
асимптотами ограничен
асимптотами 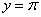 и и 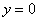 : :
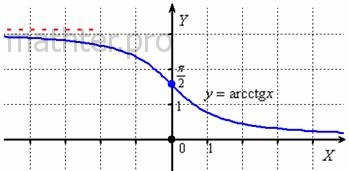
Арккотангенс тоже определён на всей числовой прямой 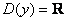 , но возвращает углы из интервала , но возвращает углы из интервала 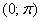 . Данная функция не является чётной или нечётной. . Данная функция не является чётной или нечётной.
Внимание! Функцию 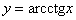 часто
машинально «принимают» за арктангенс, часто
машинально «принимают» за арктангенс,
и чтобы не «обознаться», внимательно всматривайтесь, какая функция вам дана!
Следует отметить, что две взаимно обратные функции взаимоуничтожают друг друга. Вспомним экспоненту и натуральный логарифм: 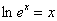 и наоборот, и наоборот, 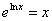 (основное логарифмическое тождество). (основное логарифмическое тождество).
С тригонометрическими функциями и «арками» то же самое, в частности:
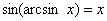 и и 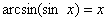 (для допустимых значений «икс») и аналогично для трёх других пар. (для допустимых значений «икс») и аналогично для трёх других пар.
Кроме того, у «арков» существуют свои формулы и взаимосвязи, но они не столь актуальны в массовой практике. Кстати, здесь к месту такой
совет:
Если ваша задача «зашла в тупик»,
то есть смысл заглянуть в математический справочник или учебник
Потому что различных фактов, правил и формул просто тьма, и это особенно характерно для геометрии и тригонометрии. Тех же тригонометрических формул – многие и
многие десятки.
 5.7. Простейшие тригонометрические уравнения 5.7. Простейшие тригонометрические уравнения
 5.5. Распространённые тригонометрические формулы 5.5. Распространённые тригонометрические формулы
| Оглавление |
|

 Кратчайший курс школьной математики
Кратчайший курс школьной математики



 5.7. Простейшие тригонометрические уравнения
5.7. Простейшие тригонометрические уравнения 5.5. Распространённые тригонометрические формулы
5.5. Распространённые тригонометрические формулы