1.6.5. Условная вероятность
Случайное событие 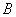 является зависимым, если помимо
случайных факторов его вероятность зависит от появления либо непоявления события является зависимым, если помимо
случайных факторов его вероятность зависит от появления либо непоявления события 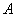 . Вероятность события . Вероятность события 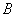 , вычисленная в предположении того, что событие , вычисленная в предположении того, что событие
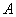 уже
произошло, называется условной вероятностью наступления события уже
произошло, называется условной вероятностью наступления события 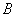 и обозначается через и обозначается через 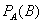 . .
При этом события 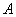 и и 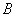 называют зависимыми событиями (хотя, строго
говоря, зависимо только одно из них). называют зависимыми событиями (хотя, строго
говоря, зависимо только одно из них).
Карты в руки:
Задача 47
Из колоды в 36 карт последовательно извлекаются 2 карты. Найти вероятность того, что вторая карта окажется червой, если до этого:
а) была извлечена черва, б) была извлечена карта другой масти.
Решение: рассмотрим событие: 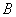 – вторая карта будет червой. Совершенно
понятно, что вероятность этого события зависит от того, черву вытянули ранее или нет. – вторая карта будет червой. Совершенно
понятно, что вероятность этого события зависит от того, черву вытянули ранее или нет.
а) Если сначала была извлечена черва (событие 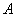 ), то в колоде осталось 35 карт, среди которых
осталось 8 карт червовой масти. По классическому определению: ), то в колоде осталось 35 карт, среди которых
осталось 8 карт червовой масти. По классическому определению:
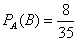 –
вероятность того, что вторая карта окажется червой при условии, что до этого была извлечена черва. –
вероятность того, что вторая карта окажется червой при условии, что до этого была извлечена черва.
б) Если же сначала была извлечена карта другой масти (событие 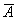 ), то все 9 черв остались в колоде. По классическому определению: ), то все 9 черв остались в колоде. По классическому определению:
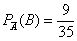 –
вероятность того, что вторая карта окажется червой при условии, что до этого была извлечена карта другой масти. –
вероятность того, что вторая карта окажется червой при условии, что до этого была извлечена карта другой масти.
Ответ: 
И здесь всё логично – если вероятность извлечения червы из полной колоды составляет 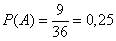 , то при извлечении следующей карты аналогичная
вероятность изменится: в первом случае – уменьшится: , то при извлечении следующей карты аналогичная
вероятность изменится: в первом случае – уменьшится: 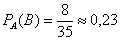 (т.к. черв стало меньше), а во втором –
возрастёт: (т.к. черв стало меньше), а во втором –
возрастёт: 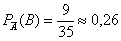 (т.к. все червы остались в колоде). (т.к. все червы остались в колоде).
Зависимых событий, разумеется, может быть и больше. Пока задача не остыла, добавим ещё одно: 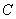 – третьей картой будет извлечена черва.
Предположим, что произошло событие – третьей картой будет извлечена черва.
Предположим, что произошло событие 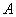 , а затем событие , а затем событие 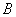 ; тогда в колоде осталось 34 карты,
среди которых 7 черв. По классическому определению: ; тогда в колоде осталось 34 карты,
среди которых 7 черв. По классическому определению:
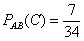 –
вероятность наступления события –
вероятность наступления события 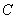 при условии, что до этого были
извлечены две червы. при условии, что до этого были
извлечены две червы.
Для самостоятельной тренировки:
Задача 48
В конверте находится 10 лотерейных билетов, среди которых 3 выигрышных. Из конверта последовательно извлекаются билеты. Найти
вероятности того, что:
а) 2-й извлечённый билет будет выигрышным, если 1-й был выигрышным;
б) 3-й будет выигрышным, если предыдущие два билета были выигрышными;
в) 4-й будет выигрышным, если предыдущие билеты были выигрышными.
Краткое решение с комментариями в конце книги.
А теперь обратим внимание на один принципиально важный момент: в рассмотренных примерах требовалось найти лишь
условные вероятности, при этом предыдущие события считались достоверно состоявшимися. Но ведь в действительности и они
являются случайными! Так, в демо-примере извлечение червы из полной колоды – есть событие случайное, вероятность которого равна 
Поэтому на практике гораздо чаще требуется отыскать вероятность совместного появления зависимых событий. Как,
например, найти вероятность события 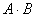 , состоящего в том, что из полной колоды
будет извлечена черва и затем ещё одна черва? Ответ на этот вопрос даёт , состоящего в том, что из полной колоды
будет извлечена черва и затем ещё одна черва? Ответ на этот вопрос даёт
 1.6.6. Теорема умножения вероятностей зависимых событий 1.6.6. Теорема умножения вероятностей зависимых событий
 1.6.4. Задачи на теоремы сложения и умножения 1.6.4. Задачи на теоремы сложения и умножения
| Оглавление |
|

 Практикум по теории вероятностей
Практикум по теории вероятностей Научись решать в считанные дни!
Научись решать в считанные дни! 1.6.6. Теорема умножения вероятностей зависимых событий
1.6.6. Теорема умножения вероятностей зависимых событий 1.6.4. Задачи на теоремы сложения и умножения
1.6.4. Задачи на теоремы сложения и умножения