1.6.4. Задачи на теоремы сложения и умножения
Этот тандем почти 100% встретится в вашей самостоятельной и отчётной работе. Хит хитов и самая настоящая классика теории
вероятностей:
Задача 41
Два стрелка сделали по одному выстрелу в мишень. Вероятность попадания для первого стрелка равна 0,8, для второго – 0,6. Найти
вероятность того, что:
а) только один стрелок попадёт в мишень;
б) хотя бы один из стрелков попадёт в мишень.
Решение: вероятность попадания / промаха одного стрелка, очевидно, не зависит от результативности
другого стрелка. Рассмотрим следующие независимые события:
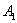 – 1-й
стрелок попадёт в мишень; – 1-й
стрелок попадёт в мишень;
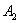 – 2-й
стрелок попадёт в мишень. – 2-й
стрелок попадёт в мишень.
По условию, 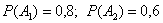 . .
Найдём вероятности противоположных событий 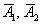 – того, что соответствующие стрелки промахнутся: – того, что соответствующие стрелки промахнутся:
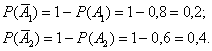
а) Рассмотрим событие: 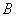 – только один стрелок попадёт в мишень. Данное
событие состоит в двух несовместных исходах: – только один стрелок попадёт в мишень. Данное
событие состоит в двух несовместных исходах:
1-й стрелок попадёт и 2-й промахнётся или
1-й промахнётся и 2-й попадёт.
На языке алгебры событий этот факт запишется следующей формулой:
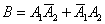
Сначала используем теорему сложения вероятностей несовместных событий, затем – теорему умножения вероятностей независимых событий:
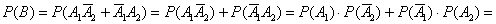
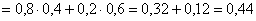 –
вероятность того, что будет только одно попадание –
вероятность того, что будет только одно попадание
б) Рассмотрим событие: 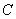 – хотя бы один из стрелков попадёт в
мишень. – хотя бы один из стрелков попадёт в
мишень.
Способ первый: событие 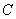 состоит в двух несовместных исходах: состоит в двух несовместных исходах:
попадёт кто-то один (событие  ) или ) или
попадут оба стрелка, обозначим последнее событие буквой 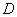 . .
Таким образом: 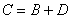
По теореме умножения вероятностей независимых событий:
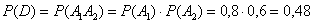 –
вероятность того, что 1-й стрелок попадёт и 2-й стрелок попадёт, –
вероятность того, что 1-й стрелок попадёт и 2-й стрелок попадёт,
и по теореме сложения вероятностей несовместных событий:
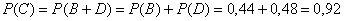 –
вероятность хотя бы одного попадания по мишени. –
вероятность хотя бы одного попадания по мишени.
Способ второй: рассмотрим противоположное событие: 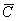 – оба стрелка
промахнутся. По теореме умножения вероятностей независимых событий: – оба стрелка
промахнутся. По теореме умножения вероятностей независимых событий:
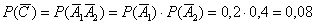
По соответствующей теореме: 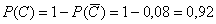
Кроме того, существует альтернативный, третий путь решения, основанный на умолчанной выше теореме сложения совместных событий:
Вероятность появления хотя бы одного из двух совместных событий 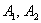 равна сумме вероятностей этих событий без
вероятности их совместного появления: равна сумме вероятностей этих событий без
вероятности их совместного появления:
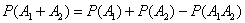
И посему способ третий: события 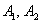 совместны, а значит, их сумма совместны, а значит, их сумма 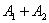 выражает событие «хотя бы
один стрелок попадёт в мишень» (см. алгебру событий). По теореме сложения вероятностей совместных
событий и теореме умножения вероятностей независимых событий: выражает событие «хотя бы
один стрелок попадёт в мишень» (см. алгебру событий). По теореме сложения вероятностей совместных
событий и теореме умножения вероятностей независимых событий:
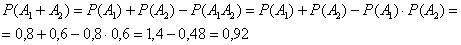
Какой способ лучше? С моей точки зрения, наиболее рационален 2-й способ, и 3-м способом я не пользуюсь вообще (т.к. нет необходимости,
да и путаница с ним бывает). Впрочем, у вас может сложиться своё мнение или пристрастие на этот счёт.
Выполним проверку: события 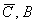 и и 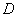 (0, 1 и 2 попадания соответственно)
образуют полную группу, поэтому сумма их
вероятностей должна равняться единице: (0, 1 и 2 попадания соответственно)
образуют полную группу, поэтому сумма их
вероятностей должна равняться единице:
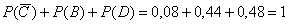 , что и
требовалось проверить. , что и
требовалось проверить.
Ответ: 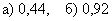
На практике часто используют «быстрый» стиль оформления и решение принимает примерно такой вид:
по условию: 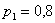 , , 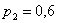 – вероятность попадания соответствующих стрелков.
Тогда вероятности их промаха: – вероятность попадания соответствующих стрелков.
Тогда вероятности их промаха:
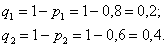
а) По теоремам сложения вероятностей несовместных и умножения вероятностей независимых событий:
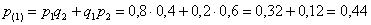 –
вероятность того, что только один стрелок попадёт в мишень. –
вероятность того, что только один стрелок попадёт в мишень.
б) По теореме умножения вероятностей независимых событий:
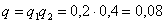 –
вероятность того, что оба стрелка промахнутся. –
вероятность того, что оба стрелка промахнутся.
Тогда: 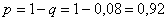 –
вероятность того, что хотя бы один из стрелков попадёт в мишень. –
вероятность того, что хотя бы один из стрелков попадёт в мишень.
Ответ: 
Однако не нужно забывать и первый вариант оформления (с росписью событий) – он хоть и длиннее, но зато содержательнее, в нём
понятнее, что, почему и зачем складывается и умножается. В ряде случаев уместен гибридный стиль, когда прописными буквами удобно
обозначить лишь некоторые события.
Контрольная задача для самостоятельного решения:
Задача 42
Для сигнализации о возгорании установлены два независимо работающих датчика. Вероятности того, что при возгорании датчик сработает, для
первого и второго датчиков соответственно равны 0,5 и 0,7. Найти вероятность того, что при пожаре:
а) оба датчика откажут, б) оба датчика сработают.
+ бонус-задание: пользуясь теоремой сложения вероятностей событий, образующих полную
группу, найти вероятность того, что при пожаре сработает только один датчик. Проверить результат прямым вычислением этой вероятности
(с помощью теорем сложения и умножения).
Здесь независимость работы устройств непосредственно прописана в условии, что, кстати, является важным уточнением. Образец решения
оформлен в академичном стиле.
Как быть, если в похожей задаче даны одинаковые вероятности, например, 0,9 и 0,9? Решать нужно точно так же! (что, собственно, уже
продемонстрировано в примере с двумя монетами). Следующий, более интересный пример тоже самостоятельно:
Задача 43
Вероятность поражения цели первым стрелком при одном выстреле равна 0,8. Вероятность того, что цель не поражена после выполнения первым
и вторым стрелками по одному выстрелу равна 0,08. Какова вероятность поражения цели вторым стрелком при одном выстреле?
Условие можно переформулировать более лаконично, но переделывать оригинал не буду – на практике приходится вникать и в более
витиеватые измышления. Образец решения оформлен «коротким» способом.
А теперь знакомьтесь – тот самый, который настрогал для вас немереное количество деталей :=)
Задача 44
Рабочий обслуживает три станка. Вероятность того, что в течение смены первый станок потребует настройки, равна 0,3, второй – 0,75,
третий – 0,4. Найти вероятность того, что в течение смены:
а) все станки потребуют настройки;
б) только один станок потребует настройки;
в) хотя бы один станок потребует настройки.
Решение: коль скоро в условии ничего не сказано о едином технологическом процессе, то работу каждого станка следует
считать независимой от работы других станков.
По аналогии с Задачей 41 здесь можно ввести в рассмотрение события 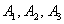 , состоящие в том, что соответствующие станки
потребуют настройки в течение смены, записать вероятности , состоящие в том, что соответствующие станки
потребуют настройки в течение смены, записать вероятности 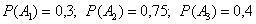 , найти вероятности противоположных событий , найти вероятности противоположных событий 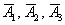 и т.д. Но с тремя
объектами так оформлять задачу уже не очень хочется – получится долго и нудно. Поэтому здесь заметно выгоднее использовать «быстрый»
стиль: и т.д. Но с тремя
объектами так оформлять задачу уже не очень хочется – получится долго и нудно. Поэтому здесь заметно выгоднее использовать «быстрый»
стиль:
По условию: 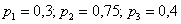 – вероятности того, что в течение смены
соответствующие станки потребуют настройки. Тогда вероятности того, что они не потребуют внимания: – вероятности того, что в течение смены
соответствующие станки потребуют настройки. Тогда вероятности того, что они не потребуют внимания:
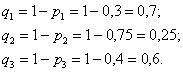
а) По теореме умножения вероятностей независимых событий:
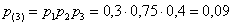 –
вероятность того, что в течение смены все три станка потребуют настройки. –
вероятность того, что в течение смены все три станка потребуют настройки.
б) Событие «В течение смены только один станок потребует настройки» состоит в трёх несовместных исходах:
1) 1-й станок потребует внимания и 2-й станок не потребует и 3-й станок не
потребует
или:
2) 1-й станок не потребует внимания и 2-й станок потребует и 3-й станок не
потребует
или:
3) 1-й станок не потребует внимания и 2-й станок не потребует и 3-й станок
потребует.
По теоремам сложения вероятностей несовместных и умножения вероятностей независимых событий:
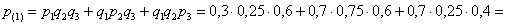
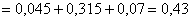 –
вероятность того, что в течение смены только один станок потребует настройки. –
вероятность того, что в течение смены только один станок потребует настройки.
Думаю, сейчас вам должно быть понятно, откуда взялось выражение 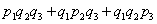
в) Вычислим вероятность 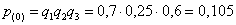 того, что станки не потребуют настройки, и затем –
вероятность противоположного события: того, что станки не потребуют настройки, и затем –
вероятность противоположного события:
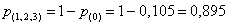 – того,
что хотя бы один станок потребует настройки. – того,
что хотя бы один станок потребует настройки.
Ответ: 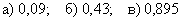
Пункт «вэ» можно решить и через сумму 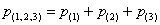 , где , где 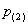 – вероятность того, что в течение смены только два
станка потребуют настройки. Это событие в свою очередь включает в себя 3 несовместных исхода, которые расписываются по аналогии с пунктом
«бэ». Постарайтесь самостоятельно найти вероятность – вероятность того, что в течение смены только два
станка потребуют настройки. Это событие в свою очередь включает в себя 3 несовместных исхода, которые расписываются по аналогии с пунктом
«бэ». Постарайтесь самостоятельно найти вероятность  , чтобы проверить всю задачу с помощью равенства , чтобы проверить всю задачу с помощью равенства
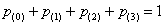 . .
Самостоятельно:
Задача 45
Из трех орудий произвели залп по цели. Вероятность попадания при одном выстреле только из первого орудия равна 0,7, из второго – 0,6, из
третьего – 0,8. Найти вероятность того, что: 1) хотя бы один снаряд попадет в цель; 2) только два снаряда попадут в цель; 3) цель будет
поражена не менее двух раз.
При основательном изучении теории вероятностей вам встретятся десятки задач милитаристского содержания, и, что характерно, после этого
никого не захочется пристрелить =) – задачи почти подарочные.
И снова о совпадениях: в том случае, если по условию два или даже все значения исходных вероятностей совпадают (например, 0,7; 0,7 и
0,7), то следует придерживаться точно такого же алгоритма решения.
Вернёмся к распространённой головоломке:
Задача 46
Стрелок попадает в цель с одной и той же вероятностью при каждом выстреле. Какова эта вероятность, если вероятность хотя бы одного
попадания при трех выстрелах равна 0,973.
Решение: обозначим через 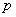 – вероятность попадания в мишень при каждом выстреле
и через – вероятность попадания в мишень при каждом выстреле
и через 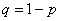 –
вероятность промаха при каждом выстреле. –
вероятность промаха при каждом выстреле.
Здесь будет удобно расписать события:
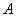 – при
3 выстрелах стрелок попадёт в мишень хотя бы один раз; – при
3 выстрелах стрелок попадёт в мишень хотя бы один раз;
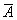 – стрелок
3 раза промахнётся. – стрелок
3 раза промахнётся.
По условию 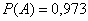 , тогда вероятность противоположного события: , тогда вероятность противоположного события:
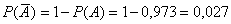
С другой стороны, по теореме умножения вероятностей независимых событий:
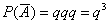
Таким образом:
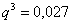
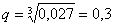 –
вероятность промаха при каждом выстреле. –
вероятность промаха при каждом выстреле.
В результате:
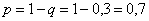 –
вероятность попадания при каждом выстреле. –
вероятность попадания при каждом выстреле.
Ответ: 0,7
Просто и изящно.
В рассмотренной задаче можно поставить дополнительные вопросы о вероятности только одного попадания, только двух попаданий и
вероятности трёх попаданий по мишени. Схема решения будет точно такой же, как и в двух предыдущих примерах:
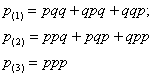
Однако принципиальное содержательное отличие состоит в том, что здесь имеют место повторные независимые испытания, которые выполняются
последовательно, независимо друг от друга и с одинаковой вероятностью исходов.
К повторным независимым испытаниям мы вернёмся чуть позже, после того, как разберём зависимые события:
 1.6.5. Условная вероятность 1.6.5. Условная вероятность
 1.6.3. Теорема умножения вероятностей независимых событий 1.6.3. Теорема умножения вероятностей независимых событий
| Оглавление |
|

 Практикум по теории вероятностей
Практикум по теории вероятностей Научись решать в считанные дни!
Научись решать в считанные дни!
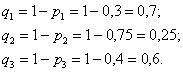
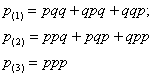
 1.6.5. Условная вероятность
1.6.5. Условная вероятность 1.6.3. Теорема умножения вероятностей независимых событий
1.6.3. Теорема умножения вероятностей независимых событий