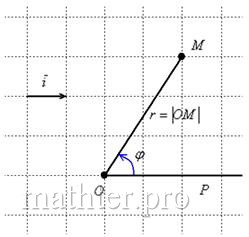
4.1. Что такое полярные координаты?

Помимо аффинной системы координат и её популярного частного случая – прямоугольной (декартовой) системы, существуют и другие подходы к построению координатной сетки плоскости и пространства. В частности, на плоскости широко распространена полярная система координат, которая невероятно удобна для решения целого спектра практических задач.

Чтобы определить полярную систему координат, достаточно зафиксировать начало координат и задать единичный координатный вектор :

Точка называется полюсом, а луч , сонаправленный с вектором – полярной осью. Графический шаблон – проще некуда, одна точка, один вектор, одна линия.

На практике вместо вектора можно где-нибудь в углу указать масштаб, например: 1 ед. = 1 см (две тетрадные клетки при ручном построении). По возможности, старайтесь выбирать именно такую, удобную во многих отношениях метрику.

А теперь мякотка:

Любая отличная от начала координат точка плоскости однозначно определяется своим расстоянием от полюса и ориентированным углом между полярной осью и отрезком . Для самого полюса , а угол не определён.

Число называют полярным радиусом точки или первой полярной координатой. Расстояние не может быть отрицательным, поэтому полярный радиус любой точки . Полярный радиус также обозначают греческой буквой («ро»).

Число называют полярным углом данной точки или второй полярной координатой. Полярный угол чаще отсчитывают в пределах (так называемые главные значения угла). Также используется диапазон и даже .

Пару называют полярными координатами точки . Из легко найти и их конкретные значения. По определению тангенса острого угла:
и сам угол: . По теореме Пифагора, , откуда находим: Таким образом, .

Один пингвин хорошо, а стая – лучше, внимательно изучаем их по чертежу:

При желании к любому отрицательно ориентированному углу можно «прикрутить» 1 оборот ( рад.) и получить удобные табличные значения:

Но недостаток этих «традиционно» ориентированных углов состоит в том, что они слишком далеко (более чем, на 180 градусов) «закручены» против часовой стрелки. Ну а в математике ценятся самые короткие и рациональные пути, не говоря уже о физике.

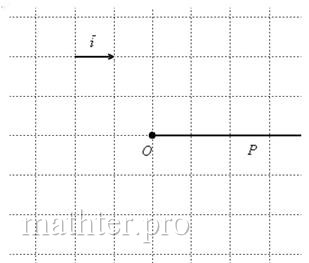
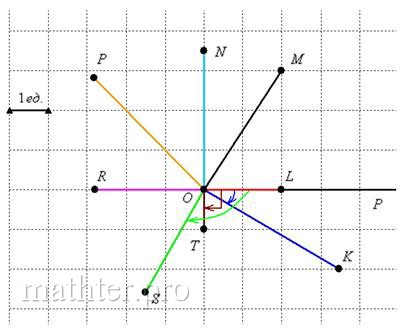
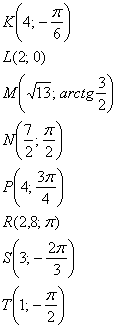
4.2. Порядок и техника построения точек в полярных координатах

3.8.3. Универсальный метод приведения

| Оглавление |

Автор: Aлeксaндр Eмeлин