5.1.2. Общее уравнение плоскости
В аффинной системе координат общее уравнение плоскости имеет вид 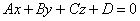 , где коэффициенты , где коэффициенты 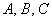 одновременно не равны
нулю. В самом общем случае, когда числа одновременно не равны
нулю. В самом общем случае, когда числа 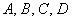 не равны нулю, плоскость пересекает все
три координатные оси, например, так: (для простоты рассмотрим привычную систему не равны нулю, плоскость пересекает все
три координатные оси, например, так: (для простоты рассмотрим привычную систему 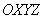 ). ).
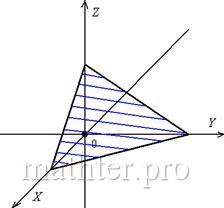
Вот, кстати, ещё одно графическое представление плоскости –
треугольник.
А теперь немного потренируем пространственное воображение. Ничего страшного, если у вас оно плохое, сейчас немного разовьём. Изобразите
в тетради декартову систему координат  (пустую)
и мысленно представляйте плоскости, о которых пойдёт речь ниже. Обязательно! – это ОЧЕНЬ важно для качественного понимания всего
дальнейшего курса!!! (пустую)
и мысленно представляйте плоскости, о которых пойдёт речь ниже. Обязательно! – это ОЧЕНЬ важно для качественного понимания всего
дальнейшего курса!!!
Начнём с простейших случаев:
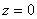
Как понимать данное уравнение? Вдумайтесь: «зет» ВСЕГДА, при любых значениях «икс» и «игрек» равно нулю. Это уравнение «родной» координатной
плоскости 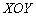 . Формально уравнение можно переписать так: . Формально уравнение можно переписать так: 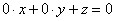 , откуда хорошо видно, что нам фиолетово, какие значения принимают «икс» и «игрек», важно,
что «зет» равно нулю. , откуда хорошо видно, что нам фиолетово, какие значения принимают «икс» и «игрек», важно,
что «зет» равно нулю.
Аналогично:
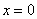 – уравнение координатной плоскости – уравнение координатной плоскости 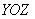 (осмысливаем почему!); (осмысливаем почему!);
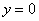 – уравнение координатной плоскости – уравнение координатной плоскости 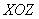 (осмысливаем почему!). (осмысливаем почему!).
Немного усложним задачу, рассмотрим плоскость 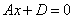 (здесь и далее в параграфе
предполагаем, что числовые коэффициенты не равны нулю). Перепишем уравнение в виде (здесь и далее в параграфе
предполагаем, что числовые коэффициенты не равны нулю). Перепишем уравнение в виде 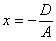 . Как его понимать? «Икс» ВСЕГДА, при любых значениях «игрек» и «зет» равно некоторому числу . Как его понимать? «Икс» ВСЕГДА, при любых значениях «игрек» и «зет» равно некоторому числу 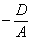 . Эта плоскость параллельна координатной плоскости . Эта плоскость параллельна координатной плоскости 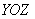 . Так, плоскость . Так, плоскость 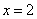 параллельна плоскости параллельна плоскости 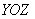 и проходит через точку и проходит через точку 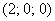 . .
Аналогично:
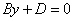 – уравнение плоскости, которая параллельна плоскости – уравнение плоскости, которая параллельна плоскости 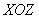 (); ();
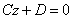 – уравнение плоскости, которая параллельна плоскости – уравнение плоскости, которая параллельна плоскости 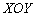 . .
Осмысливаем! И добавляем членов: 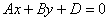 . Это уравнение можно переписать так: . Это уравнение можно переписать так: 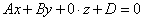 , то есть «зет» может быть любым. Что это значит? «Икс» и «игрек» связаны
соотношением , то есть «зет» может быть любым. Что это значит? «Икс» и «игрек» связаны
соотношением 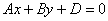 , которое «прочерчивает» в плоскости , которое «прочерчивает» в плоскости 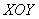 некоторую прямую (узнаёте уравнение прямой на
плоскости?). Поскольку «зет» может быть любым, то эта прямая «тиражируется» на любой высоте. Таким образом, уравнение некоторую прямую (узнаёте уравнение прямой на
плоскости?). Поскольку «зет» может быть любым, то эта прямая «тиражируется» на любой высоте. Таким образом, уравнение 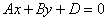 определяет плоскость, параллельную координатной оси определяет плоскость, параллельную координатной оси 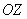
Аналогично:
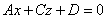 – уравнение плоскости, которая параллельна оси – уравнение плоскости, которая параллельна оси 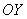 (почему?); (почему?);
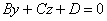 – уравнение плоскости, которая параллельна оси – уравнение плоскости, которая параллельна оси 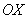 (почему?). (почему?).
Если свободные члены 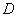 нулевые, то эти плоскости будут непосредственно
проходить через соответствующие оси. Например, классическая «прямая пропорциональность»: нулевые, то эти плоскости будут непосредственно
проходить через соответствующие оси. Например, классическая «прямая пропорциональность»: 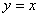 . Начертите в плоскости . Начертите в плоскости 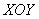 прямую прямую 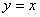 и мысленно размножьте её вверх и вниз (так как «зет» любое). Вывод: плоскость, заданная
уравнением и мысленно размножьте её вверх и вниз (так как «зет» любое). Вывод: плоскость, заданная
уравнением 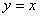 , проходит через координатную ось , проходит через координатную ось 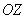 . .
Завершаем обзор: плоскость 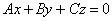 проходит через начало координат. Ну, здесь
совершенно очевидно, что точка проходит через начало координат. Ну, здесь
совершенно очевидно, что точка 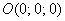 удовлетворяет данному уравнению. удовлетворяет данному уравнению.
И, наконец, случай, который изображён на чертеже выше: 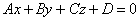 – данная
плоскость дружит со всеми координатными осями, при этом она всегда «отсекает» треугольник, который может располагаться в любом из восьми октантов
(координатные плоскости системы – данная
плоскость дружит со всеми координатными осями, при этом она всегда «отсекает» треугольник, который может располагаться в любом из восьми октантов
(координатные плоскости системы 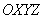 делят пространство на 8 равных
частей – октантов). делят пространство на 8 равных
частей – октантов).
И пока у вас разогретое пространственное воображение :), совсем кратко о линейных неравенствах, хотя по логике изложения, они здесь немного не к
месту:
 5.1.3. Линейные неравенства в пространстве 5.1.3. Линейные неравенства в пространстве
 5.1.1. Понятие плоскости в пространстве 5.1.1. Понятие плоскости в пространстве
| Оглавление |
|

 Аналитическая геометрия для «чайников»
Аналитическая геометрия для «чайников»
 5.1.3. Линейные неравенства в пространстве
5.1.3. Линейные неравенства в пространстве 5.1.1. Понятие плоскости в пространстве
5.1.1. Понятие плоскости в пространстве