5.1.3. Линейные неравенства в пространстве
Всё очень похоже на «плоский» случай.
Если уравнение 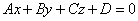 задаёт плоскость пространства, то неравенства задаёт плоскость пространства, то неравенства 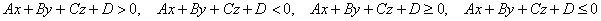 определяют полупространства. Если неравенство
нестрогое (два последних в списке), то в его решение кроме полупространства входит и сама плоскость. определяют полупространства. Если неравенство
нестрогое (два последних в списке), то в его решение кроме полупространства входит и сама плоскость.
Как и для линейных неравенств плоскости, справедлив аналогичный принцип: если одна точка
полупространства удовлетворяет неравенству, то и ВСЕ точки этого полупространства удовлетворяют данному неравенству.
Читайте примеры и посматривайте на ту же систему 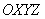 в тетради: в тетради:
1) 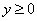 . Как понимать это неравенство? «Икс» и «зет» могут быть любыми, а вот
«игрек» всегда больше либо равно нулю. Данное неравенство определяет правое полупространство; так как оно нестрогое, то координатная плоскость . Как понимать это неравенство? «Икс» и «зет» могут быть любыми, а вот
«игрек» всегда больше либо равно нулю. Данное неравенство определяет правое полупространство; так как оно нестрогое, то координатная плоскость 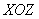 входит в решение. входит в решение.
2) 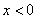 – «игрек» и «зет» могут быть любыми, а вот «икс» строго меньше нуля.
Неравенство задаёт дальнее от нас полупространство, и ввиду его строгости, координатная плоскость – «игрек» и «зет» могут быть любыми, а вот «икс» строго меньше нуля.
Неравенство задаёт дальнее от нас полупространство, и ввиду его строгости, координатная плоскость 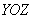 не входит в решение. не входит в решение.
3) 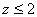 Сначала мысленно начертим плоскость Сначала мысленно начертим плоскость 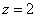 – данная плоскость параллельна «родной» координатной плоскости – данная плоскость параллельна «родной» координатной плоскости 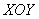 и расположена на высоте и расположена на высоте 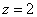 (на 2 единицы
выше плоскости (на 2 единицы
выше плоскости 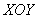 ). При любых «икс» и «игрек» – «зет» меньше либо равно двум.
Поэтому неравенство определяет нижнее полупространство + саму плоскость ). При любых «икс» и «игрек» – «зет» меньше либо равно двум.
Поэтому неравенство определяет нижнее полупространство + саму плоскость 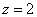 . .
4) 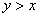 – мысленно представляем «прямую пропорциональность» – плоскость, которая
проходит через ось – мысленно представляем «прямую пропорциональность» – плоскость, которая
проходит через ось 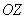 . И если «игрек» должен быть больше,
чем «икс» («зет» – любое), то этому условию соответствуют все точки дальнего от нас полупространства, при этом плоскость . И если «игрек» должен быть больше,
чем «икс» («зет» – любое), то этому условию соответствуют все точки дальнего от нас полупространства, при этом плоскость 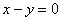 не входит в решение. не входит в решение.
5) Дана плоскость 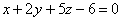 . Я специально подобрал плоскость, которая «высекает»
треугольник в первом октанте (такой, как на чертеже выше). Требуется строгим неравенством задать полупространство, которое содержит начало
координат. . Я специально подобрал плоскость, которая «высекает»
треугольник в первом октанте (такой, как на чертеже выше). Требуется строгим неравенством задать полупространство, которое содержит начало
координат.
Решение: составим вспомогательный многочлен 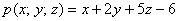 и вычислим его
значение в начале координат: и вычислим его
значение в начале координат: 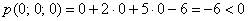 , таким образом, искомое неравенство: , таким образом, искомое неравенство: 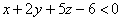 . .
Система линейных неравенств определяет некоторую область пространства. Она может быть ограниченной или не ограниченной. Любая точка области решений обязательно удовлетворяет каждому неравенству системы. Так, система:
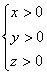 – определяет первый координатный октант, и любая точка этого октанта
удовлетворяет каждому неравенству системы (т.к. имеет положительные координаты). Это пример неограниченной области решения. – определяет первый координатный октант, и любая точка этого октанта
удовлетворяет каждому неравенству системы (т.к. имеет положительные координаты). Это пример неограниченной области решения.
Пространственное понимание уравнений и неравенств крайне полезно не только в аналитической геометрии, но и для решения других задач высшей
математики. И поэтому мы прямо сейчас закрепим эту чрезвычайно важную тему:
 5.1.4. Как построить плоскость? 5.1.4. Как построить плоскость?
 5.1.2. Общее уравнение плоскости 5.1.2. Общее уравнение плоскости
| Оглавление |
|

 Аналитическая геометрия для «чайников»
Аналитическая геометрия для «чайников» 5.1.4. Как построить плоскость?
5.1.4. Как построить плоскость? 5.1.2. Общее уравнение плоскости
5.1.2. Общее уравнение плоскости