|
Ваш репетитор, справочник и друг!
|
5.6.4. Как найти угол между прямой и плоскостью?д) Логическое продолжение темы. Если прямая Продолжим эксплуатацию геометрического инвентаря: Используем формулу синуса угла между прямой и плоскостью: Таким образом, для нахождения искомого угла достаточно знать лишь нормальный вектор плоскости и направляющий вектор прямой. Скалярное произведение векторов уже найдено в пункте «а»: Вычислим длины векторов: По формуле: На иррациональность в знаменателе забиваем, поскольку нам нужен сам угол: Выложим в ряд головы очередного Змея-Горыныча: Ответ: а) б) в) г) д) Переходим к рассмотрению частного случая – когда:
|
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Аналитическая геометрия для «чайников»
Аналитическая геометрия для «чайников»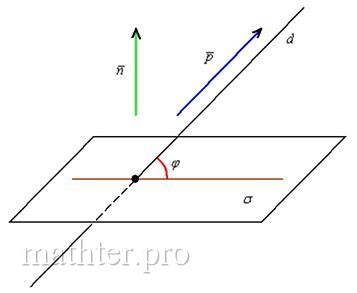
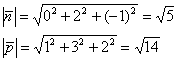
 5.6.5. Прямая перпендикулярна плоскости
5.6.5. Прямая перпендикулярна плоскости 5.6.3. Как найти проекцию прямой на плоскость?
5.6.3. Как найти проекцию прямой на плоскость?