|
Ваш репетитор, справочник и друг!
|
5.6.2. Как найти точку пересечения прямой и плоскости?Ответим на этот (и не только) вопрос на конкретном примере, я постарался собрать в одной задаче всё, что связано с этой точкой: Задача 162 Дана прямая а) доказать, что прямая пересекает плоскость; в) через прямую г) найти проекцию прямой д) найти угол между прямой НеслАбо. А ведь всё началось с единственной точки пересечения =) Решение: сначала закрепим задачу о взаимном расположении прямой и плоскости: а) Из уравнений прямой находим принадлежащую ей точку и направляющий вектор: Вектор нормали плоскости, как всегда, сдаётся без боя: Вычислим скалярное произведение: б) Найдём точку пересечения плоскости и прямой: Приём решения стандартен и неоднократно применялся в
предыдущем параграфе. Сначала перепишем уравнения прямой в параметрической форме: Точка С другой стороны, точка Раскрываем скобки, приводим подобные слагаемые и находим «тэ нулевое»: Самостоятельно выполните устную проверку – подставьте координаты точки в уравнение плоскости и в уравнения прямой. Они должны «подойти» и там и там. в) Найдём уравнение плоскости Выполним схематический чертёж: Уравнение плоскости В качестве точки, принадлежащей прямой «дэ», не возбраняется, конечно, взять найденную в предыдущем пункте точку пересечения Уравнение плоскости «омега» составим по точке Таким образом: Проверка опять же простая: 1) Мысленно вычислим скалярное произведение нормальных векторов 2) Теперь нужно убедиться, что прямая «дэ» действительно лежит в найденной плоскости «омега». Можно использовать типовой алгоритм, но тут есть быстрое решение – устно подставляем координаты двух известных точек
|
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Аналитическая геометрия для «чайников»
Аналитическая геометрия для «чайников»
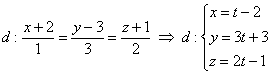
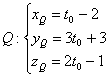 , или одной строчкой:
, или одной строчкой: 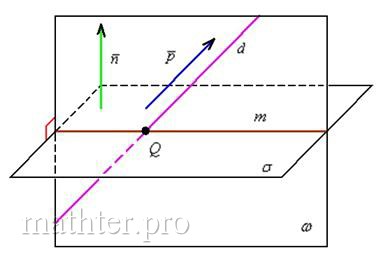
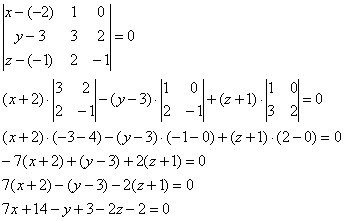
 5.6.3. Как найти проекцию прямой на плоскость?
5.6.3. Как найти проекцию прямой на плоскость? 5.6.1. Взаимное расположение прямой и плоскости
5.6.1. Взаимное расположение прямой и плоскости