|
Ваш репетитор, справочник и друг!
|
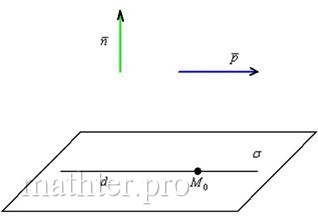
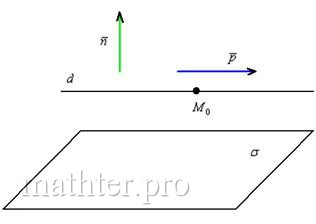
5.6.1. Взаимное расположение прямой и плоскостиРассмотрим плоскость Существует три варианта взаимного расположения прямой и плоскости: 1) прямая пересекает плоскость в некоторой точке 2) прямая параллельна плоскости: 3) прямая лежит в плоскости: Как выяснить взаимное расположение прямой и плоскости?Это заметно проще, чем выяснить взаимное расположение двух прямых.Изучим аналитические условия, которые позволят нам ответить на данный вопрос. Выполним схематический чертёж, на котором прямая пересекает плоскость: 1) Прямая пересекает плоскость тогда и только тогда, когда её направляющий вектор В координатах это условие запишется следующим образом: Если же данные векторы ортогональны, то их скалярное произведение равно нулю: Разграничим эти случаи: 2) Если прямая параллельна плоскости (рисунок внизу слева), то любая точка 3) Если прямая лежит в плоскости (рис. справа) то любая точка Алгоритм выяснения взаимного расположения прямой и плоскости достаточно примитивен – всего в два шага. Кроме того, оформляя задачи, можно обойтись вообще без составления системы: Задача 160 Выяснить взаимное расположение прямой, заданной точкой Решение: вытащим нормальный вектор плоскости: Вычислим скалярное произведение вектора нормали плоскости и направляющего вектора прямой: Подставим координаты точки Получено верное равенство, следовательно, точка Ответ: прямая лежит в плоскости Самостоятельно: Задача 161 Выяснить взаимное расположение плоскости Решение и ответ в конце книги. И после небольшой разминки начинаем накидывать «блины» на штангу:
|
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Аналитическая геометрия для «чайников»
Аналитическая геометрия для «чайников»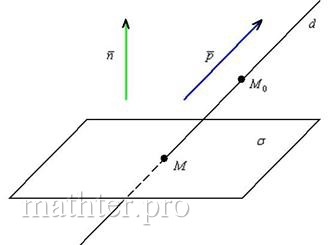
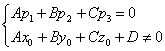
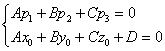
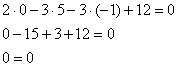
 5.6.2. Как найти точку пересечения прямой и плоскости?
5.6.2. Как найти точку пересечения прямой и плоскости? 5.5.10. Параллельные прямые в пространстве
5.5.10. Параллельные прямые в пространстве