|
Ваш репетитор, справочник и друг!
|
5.5.1. Взаимное расположение прямыхДве прямые 1) скрещиваться; 2) пересекаться в точке 3) быть параллельными 4) совпадать. Случай № 1 принципиально отличается от других случаев. Две прямые скрещиваются, если они не лежат в одной плоскости. Поднимите одну руку вверх, а другую руку вытяните вперёд – вот вам и пример скрещивающихся прямых. В пунктах же № 2-4 прямые обязательно лежат в одной плоскости. Как выяснить взаимное расположение прямых в пространстве?Рассмотрим общий алгоритм и две прямые: Для лучшего понимания выполним схематический чертёж, на котором в качестве примера изображены скрещивающиеся прямые 1) Если прямые скрещиваются, то векторы Пусть 2) Если направляющие векторы 3-4) Если направляющие векторы …Всё ли вам понятно? Если нет, то милости прошу по ссылкам, если да, то отработаем этот незатейливый алгоритм на конкретных практических примерах: Задача 153 Выяснить взаимное расположение двух прямых Решение: как и во многих задачах, решение удобно оформить по пунктам: 1) Вытаскиваем из уравнений прямых их точки и направляющие векторы: 2) Найдём вектор: 3) Вычислим смешанное произведение векторов: Таким образом, векторы 4) Проверим направляющие векторы Составим систему из соответствующих координат данных векторов: Из каждого уравнения следует, что 5) Выясним, есть ли у прямых общие точки. Возьмём точку Получены неверные равенства, значит, точка «не подошла». Таким образом, общих точек у прямых нет, и им ничего не остаётся, как быть параллельными. Ответ: Интересный пример для самостоятельного решения: Задача 154 Выяснить взаимное расположение прямых Обратите внимание, что у второй прямой в качестве параметра выступает буква Решение и ответ в конце книги. Далее мы по порядку рассмотрим задачи, «посвященные» скрещивающимся прямым, затем – пересекающимся, затем – параллельным и совпадающим:
|
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Аналитическая геометрия для «чайников»
Аналитическая геометрия для «чайников»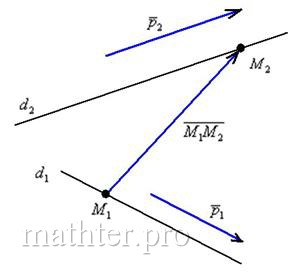 Так как известны точки
Так как известны точки 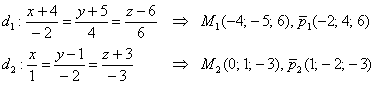
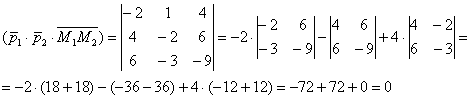
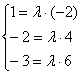
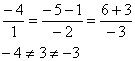
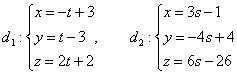
 5.5.2. Скрещивающиеся прямые
5.5.2. Скрещивающиеся прямые 5.4.4. Прямая, заданная пересечением двух плоскостей
5.4.4. Прямая, заданная пересечением двух плоскостей