|
Ваш репетитор, справочник и друг!
|
5.5.2. Скрещивающиеся прямыеНапоминаю, что прямые скрещиваются, если не существует плоскости, в которой бы они обе лежали. Когда я продумывал практику, в голову пришла задача-монстр, и сейчас рад представить вашему вниманию дракона с четырьмя головами: Задача 155 Даны прямые а) доказать, что прямые скрещиваются; б) найти уравнения прямой в) составить уравнения прямой г) найти расстояние Дорогу осилит идущий, решение: а) Докажем, что прямые скрещиваются. Найдём точки и направляющие векторы данных прямых: Найдём вектор Вычислим смешанное произведение векторов: б) Найдём уравнения прямой Для разнообразия я разместил прямую Что известно о прямой «дэ»? Известна принадлежащая ей точка А это уже знакомый из Задачи 151 мотив, найдём их векторное произведение: Уравения искомой прямой составим по точке Готово. В принципе, можно сменить знаки в знаменателях и записать уравнения в виде Для проверки нужно подставить координаты точки
|
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Аналитическая геометрия для «чайников»
Аналитическая геометрия для «чайников»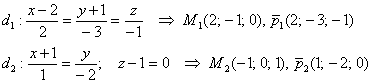
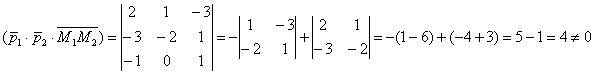 , таким образом, векторы
, таким образом, векторы 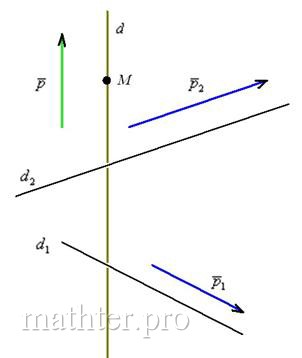
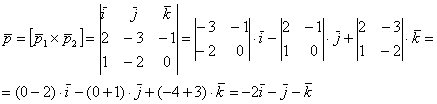
 5.5.3. Как найти прямую, содержащую общий перпендикуляр?
5.5.3. Как найти прямую, содержащую общий перпендикуляр? 5.5.1. Взаимное расположение прямых
5.5.1. Взаимное расположение прямых