|
Ваш репетитор, справочник и друг!
|
5.5.3. Как найти прямую, содержащую общий перпендикуляр?в) Эта задачка посложнее будет. «Чайникам» рекомендую пропустить данный пункт, не хочу охлаждать вашу искреннюю симпатию к
аналитической геометрии =) Кстати, и более подготовленным читателям, возможно, лучше тоже повременить – дело в том, что по сложности эту задачу
надо бы поставить последней в параграфе, но по логике изложения она должна располагаться здесь. …Впрочем, Итак, требуется найти уравнения прямой Общий перпендикуляр скрещивающихся прямых – это отрезок, соединяющий данные прямые и перпендикулярный данным прямым: Вот наш красавец: Что известно о прямой «эм»? Известен её направляющий вектор Но есть хитрый ход, связанный с использованием параметрических уравнений прямой. Решение оформим по пунктам: 1) Перепишем уравнения первой прямой в параметрической форме: Рассмотрим точку Жизнь налаживается, одна неизвестная – это всё-таки не три неизвестных. 2) Аналогичные действия проведём со второй прямой. Перепишем её уравнения в параметрическом
виде: Если точка 3) Запишем вектор
4) Вектор Получилась самая, что ни на есть обычная система линейных уравнений с тремя неизвестными Из 2-го уравнения выразим То, что значения параметров получились одинаковыми – чистая случайность. 5) Небо полностью проясняется, подставим найденные значения Сам вектор И после длинного пути всегда интересно выполнить проверку. Подставим координаты точки Подставим координаты Вывод: найденные точки действительно принадлежат соответствующим прямым. 6) Заключительный аккорд: составим уравнения прямой В принципе, можно подобрать «хорошую» точку с целыми координатами, но это уже косметика.
|
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Аналитическая геометрия для «чайников»
Аналитическая геометрия для «чайников»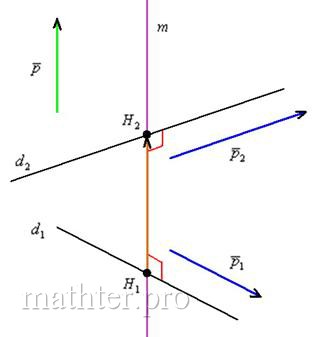
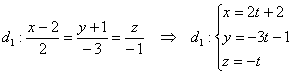
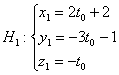 , или:
, или: 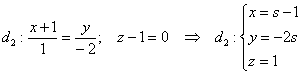
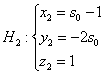 , или:
, или: 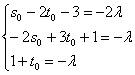
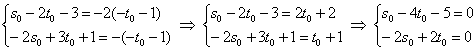
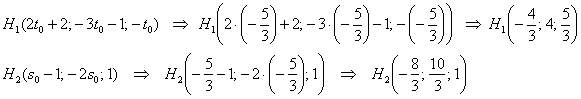
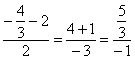
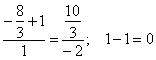
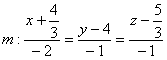
 5.5.4. Как найти расстояние между скрещивающимися прямыми?
5.5.4. Как найти расстояние между скрещивающимися прямыми? 5.5.2. Скрещивающиеся прямые
5.5.2. Скрещивающиеся прямые