|
Ваш репетитор, справочник и друг!
|
1.10. Формула ПуассонаЕсли количество независимых испытаний Утопичная, конечно, задача, но что делать – таких много:) Задача 72 Решение: в данном случае количество «испытаний» Вычислим: Таким образом: Ответ: С технической точки зрения результат 1) С помощью специальной таблицы, которая до сих пор встречается в некоторых книгах. В данную таблицу сведены различные значения 2) С помощью прямого вычисления на микрокалькуляторе (прогресс!), именно этим способом я и провёл вычисления. 3) С помощью стандартной экселевской функции: ПУАССОН(m; лямбда; 0), Следует отметить, что развитие вычислительной техники фактически отправило в историю рассмотренное решение – по той причине, что ответ легко вычислить более точно* по формуле Бернулли, например, с помощью функции БИНОМРАСПприложения MS Excel: * и, разумеется, существует абсолютно точное значение с длинным «хвостом». Но формула Пуассона, тем не менее, даёт очень крутое приближение: Впрочем, это всё лирика, решать-то всё равно нужно по формуле Пуассона, пока я и мои коллеги не написали для вас новые учебники:) Ну а пока классика жанра: Задача 73 Решение: используем формулу Пуассона: а) б) в) Приём уже знаком – «заходим с чёрного хода». Сначала найдём И по теореме сложения вероятностей противоположных событий: Ответ: а) Само собой, ручками это всё считать надоест, и поэтому я добавил в Калькулятор (Пункт 7) автоматическое вычисление этих вероятностей. Следующий пример самостоятельно; по возможности, проведите вычисления несколькими способами: Задача 74 Иногда условие встречается в несколько другой интерпретации. Так, в предложенной задаче может идти речь о том, что производственный брак составляет 0,1% или, например, «в среднем 0,8 детали на каждую тысячу». Обратите внимание, что в последнем случае нам дано готовое значение «лямбда». Ни в коем случае не отключаем голову – даже в таких простых примерах! Ещё раз подчёркиваю, что формула Пуассона лишь приближает формулу Бернулли, и на самом деле это её не единственное применение. В следующей главе мы познакомимся с распределением Пуассона и разберём другие задачи с этой формулой.
|
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Практикум по теории вероятностей
Практикум по теории вероятностей Научись решать в считанные дни!
Научись решать в считанные дни!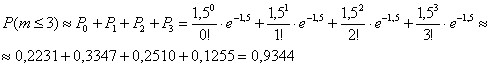
 1.11. Локальная теорема Лапласа
1.11. Локальная теорема Лапласа 1.9. Независимые испытания и формула Бернулли
1.9. Независимые испытания и формула Бернулли