Ваш репетитор, справочник и друг!

Практикум по теории вероятностей

Научись решать в считанные дни!

1.9. Независимые испытания и формула Бернулли

Что такое независимые испытания? Практически всё понятно уже из самого названия. Пусть производится несколько испытаний. Если вероятность появления некоего события в каждом из них не зависит от исходов остальных испытаний, то… заканчиваем фразу самостоятельно! При этом под словосочетанием «независимые испытания» часто подразумевают повторные независимые испытания – когда они осуществляются друг за другом. Простейшие примеры:

– монета подбрасывается 10 раз;
– игральная кость подбрасывается 20 раз.

Совершенно ясно, что вероятность выпадения орла либо решки в любом испытании не зависит от результатов других бросков. Аналогичное утверждение, естественно, справедливо и для кубика. А вот последовательное извлечение карт из колоды не является серией независимых испытаний – очевидно, это цепочка зависимых событий. Однако если карту каждый раз возвращать обратно, то это тоже будут повторные независимые испытания.

И у нас в гостях очередной Терминатор, который абсолютно равнодушен к своим удачам / неудачам, и поэтому его стрельба представляет собой образец стабильности :)

Задача 65
Стрелок совершает 4 выстрела по мишени. Вероятность попадания при каждом выстреле постоянна и равна . Найти вероятность того, что:
а) стрелок попадёт только один раз, б) стрелок попадёт 2 раза.

Решение: условие сформулировано в общем виде и вероятность попадания в мишень при каждом выстреле считается известной. Она равна (если совсем тяжко, присвойте параметру какое-нибудь конкретное значение, например, ).

Коль скоро мы знаем , то легко найти вероятность промаха в каждом выстреле:
, то есть, «ку» – это тоже известная нам величина.

а) Рассмотрим событие «Стрелок попадёт только один раз» и обозначим его вероятность через (индексы понимаются как «1 попадание из 4»). Данное событие состоит в 4 несовместных исходах: стрелок попадёт в 1-й или во 2-й, или в 3-й, или в 4-й попытке. По теоремам сложения вероятностей несовместных и умножения вероятностей независимых событий:

Упростим результат с помощью комбинаторной формулы количества сочетаний:
способами можно выбрать попытку, в которой стрелок попал, и, поскольку в каждом исходе имеет место 1 попадание и 3 промаха, то:
– вероятность того, что стрелок попадёт только 1 раз из 4.

…как-то так «с лёгкой руки» я начал называть повторные независимые испытания «попытками», что не в каждой задаче может быть корректным в содержательном плане… …ну да ладно.
б) Рассмотрим событие «Стрелок попадёт два раза» и обозначим его вероятность через («2 попадания из 4»). Здесь исходов будет уже больше, попадания возможны:

в 1-й и 2-й попытках
или
в 1-й и 3-й попытках,
или
в 1-й и 4-й попытках,
или
во 2-й и 3-й попытках,
или
во 2-й и 4-й попытках,
или
в 3-й и 4-й попытках.

Таким образом, по тем же теоремам сложения и умножения вероятностей:

Можно ли так решать задачу? Безусловно, можно. Но что делать, если серия состоит из 5, 6 или бОльшего количества выстрелов? Тут уже будут получаться десятки слагаемых, запись которых отнимет много времени и места. В этой связи гораздо рациональнее придерживаться более компактной схемы:
способами (перечислены выше) можно выбрать 2 попытки, в которых произойдут попадания.

И, поскольку в любом исходе ровно 2 попадания и 2 промаха, то:
– вероятность того, что стрелок попадёт 2 раза из 4.

Ответ:

Итак – вероятность того, что будет 1 попадание из 4, равна , вероятность того, что будет 2 попадания из 4, равна , …не замечаете ли вы закономерности?

Только что на конкретном примере мы повторили путь Якоба Бернулли, который несколько веков назад вывел формулу, названную позже в его честь:

Вероятность того, что в независимых испытаниях некоторое случайное событие наступит ровно раз, равна:

, где:

– вероятность появления события в каждом испытании;
– вероятность непоявления события в каждом испытании,

при этом коэффициент часто называют биномиальным коэффициентом.

За примером далеко ходить не будем:

Задача 66
Найти вероятность того, что при 10 бросках монеты орёл выпадет 3 раза.

Решение: сначала немного порассуждаем: всего проводится 10 повторных независимых испытаний. Сколькими способами можно выбрать 3 испытания из 10, в которых выпадет орёл? Считаем:
способами.

Это что же получается, нужно записывать 120 слагаемых, в каждом из которых 10 множителей?! Конечно, нет! – ведь есть формула Бернулли:

, в данном случае:

– всего испытаний;
– количество испытаний, в которых должен появиться орёл;
– вероятность появления орла в каждом испытании;
– вероятность появления решки в каждом испытании.

Таким образом:
– вероятность того, что при 10 бросках монеты орёл выпадет ровно 3 раза.

Ответ:

Следует отметить, что повторный характер независимых испытаний не является «жизненно важным» условием для применения формулы Бернулли. Рассмотрим похожую задачу:
Найти вероятность того, что при броске 10 монет орёл выпадет на 3 монетах.

Здесь испытания не повторяются, а скорее, производятся одновременно, но, тем не менее, работает та же самая формула: .

Решение будет отличаться смыслом и некоторыми комментариями, в частности:
способами можно выбрать 3 монеты, на которых выпадет орёл.
– вероятность выпадения орла на каждой из 10 монет
и т.д.

Однако на практике подобные задачи встречаются не столь часто, и, видимо, по этой причине формула Бернулли чуть ли не стереотипно ассоциируется только с повторными испытаниями. Хотя, как только что было показано, повторяемость вовсе не обязательна.
Следующая задача для самостоятельного решения:

Задача 67
Игральную кость бросают 6 раз. Найти вероятность того, что 5 очков:

а) не выпадут (выпадут 0 раз);
б) выпадут 2 раза;
в) выпадут 5 раз.

Результаты округлить до 4 знаков после запятой.

Очевидно, что в рассматриваемых примерах некоторые события более вероятны, а некоторые – менее вероятны. Так, например, при 6 бросках кубика даже безо всяких расчётов интуитивно понятно, что вероятности событий пунктов «а» и «бэ» значительно больше вероятности того, что «пятёрка» выпадет 5 раз. И на уровне интуиции легко сделать вывод, что наивероятнейшее количество появлений «пятёрки» равно единице – ведь всего граней шесть, и при 6 бросках кубика каждая из них должна выпасть в среднем по одному разу. Желающие могут вычислить вероятность и посмотреть, будет ли она больше «конкурирующих» значений и .

Теперь сформулируем строгий критерий на этот счёт:

Для отыскания наивероятнейшего числа появлений случайного события в независимых испытаниях (с вероятностью в каждом испытании) руководствуются следующим двойным неравенством:

, причём:

1) если значение – дробное, то существует единственное наивероятнейшее число ;
в частности, если – целое, то оно и есть наивероятнейшее число: ;

2) если же – целое, то существуют два наивероятнейших числа: и .

Найдём наивероятнейшее число появлений «пятёрки» при 6 бросках кубика. Сначала вычислим:
– целое число, таким образом, это частный случай 1-го пункта и .
Как вариант, можно воспользоваться общей формулой:

– полученному неравенству удовлетворяет единственное целое значение .
В целях закрепления материала решим пару задач:

Задача 68
Вероятность того, что при броске мяча баскетболист попадёт в корзину, равна 0,3. Найти наивероятнейшее число попаданий при 8 бросках и соответствующую вероятность.

Решение: для оценки наивероятнейшего числа попаданий используем двойное неравенство . В данном случае:

– всего бросков;
– вероятность попадания в корзину при каждом броске;
– вероятность промаха при каждом броске.

Таким образом, наивероятнейшее количество попаданий при 8 бросках находится в следующих пределах:

Поскольку левая граница (1,7) – дробное число (пункт № 1 критерия – см. выше), то существует единственное наивероятнейшее значение, и, очевидно, что это .

Используя формулу Бернулли , вычислим вероятность того, что при 8 бросках будет ровно 2 попадания:

Ответ: – наивероятнейшее количество попаданий при 8 бросках, – соответствующая вероятность.

Аналогичное задание для самостоятельного решения:

Задача 69
Монета подбрасывает 9 раз. Найти вероятность наивероятнейшего числа появлений орла

Решение и ответ в конце книги.

А сейчас немного отвлёчёмся и рассмотрим весьма любопытную ситуацию: предположим, что во всех 9 испытаниях выпал орёл. Что, кстати, не являются каким-то уж сильно невероятным событием: ;-)

Вопрос: какая сторона монеты вероятнее всего выпадет в 10-м испытании?

Как вы думаете?

…ответьте на этот вопрос и перейдите на следующую страницу.

Правильный ответ: вероятности останутся равными! Почему? Причина была сформулирована в начале параграфа: поскольку испытания независимы, то вероятность выпадения орла либо решки в любом испытании не зависит от результатов других испытаний!

Однако игры разума таковы, что у многих людей напрашивается следующий вывод: раз орёл выпал много раз подряд, то теперь выпадение решки гораздо (!) вероятнее. Этот психологический феномен получил название Ошибка игрока. Если подбрасывать монету тысячи, десятки тысяч раз, то соотношение орлов / решек будет примерно равным (о чём мы ещё поговорим). Но в этом процессе неоднократно встретятся эпизоды, когда монету «заклинит» на какой-то одной грани, и КАК ИМЕННО распределятся эти «необычные» серии на длинной дистанции – никто не знает.

К слову, о «необычности». Любая случайная последовательность девяти орлов/решек так же вероятна, как и выпадение 9 орлов! Проверить данный факт легче лёгкого: запишем произвольную последовательность исходов, например:
Орёл/Решка/Решка/Орёл /Решка/ Орёл /Решка/ Орёл /Орёл

По теореме умножения вероятностей независимых событий, вероятность появления этой цепочки:
, что в точности равно вероятности выпадения девяти орлов !

И здесь мы сталкиваемся со второй иллюзией – человек склонен считать «красивые» комбинации чем-то из ряда вон выходящим и чуть ли не фантастическим. Но на самом деле ничего необычного, например, в комбинации О/О/О/Р/Р/Р/О/О/О – нет, и она может запросто появиться в серии испытаний.

Вероятность получить, скажем, пиковый «Ройял-флеш» в покересоставляет 1:2598960, однако мало кто задумывается, что с той же вероятностью приходит ЛЮБАЯ, в том числе, совершено «мусорная» комбинация из пяти карт! И с этой точки зрения «сверхъестественная» комбинация 10, В, Д, К, Т пик ничем не примечательна – встречалась «в истории» наряду с другими очень много раз. И поэтому «Ройял-флеш» может запросто оказаться у вас или у вашего соперника.

Кстати, к теме нашего разговора относятся и типичные ситуации в играх, в частности, в картах – когда «карта идёт», и наоборот – когда постоянно сдают «один мусор» или «фатально не везёт». Такие «полосы» встречаются у каждого игрока, и никакой мистики в этом нет. Да что там игры, в жизни то же самое – пресловутые «чёрные и белые полосы».

На просторах Интернета часто встречается популярный «секрет выигрыша» в рулетку, известный также под названием «Мартингейл». Краткая суть системы состоит в следующем: «Ставьте на красное. Если выпало чёрное, удваивайте ставку и снова ставьте на красное. Если снова выпало чёрное, то ещё раз удваивайте ставку и снова ставьте на красное и т.д.». Казалось бы – вот оно, золотое дно, ведь красных секторов целых 18 из 37! (+ 18 черных и 1 зеро в европейской рулетке). И уж «красное» должно (!) выпасть если не на 5-й, то на 10-й раз точно, что позволит отыграть всё ранее поставленное с прибылью!

Ничего подобного!

Вероятность выпадения красного сектора в любом испытании постоянна и никак не зависит от результатов предыдущих испытаний. Постоянна – и проигрышна (т.к. поставленные на «красное» деньги с вероятностью проигрываются, а в случае успеха удваиваются). Длинная серия «чёрного» обязательно появятся (рано или поздно) и разорит даже Билла Гейтса. Поэтому данный «секрет», как и все остальные системы игры в рулетку – не работает.

«Ошибка игрока» совершается и многими участниками лотерей. Она состоит в том, что люди пытаются предугадать числа на основе статистики предыдущих тиражей. Чистой воды химера и пустая трата времени – если, например, № 8 не выпадал 50 раз подряд, то он с таким же успехом может не выпасть ещё 150 раз (это не ирония). Однако если провести десятки тысяч тиражей, то количество появлений всех номеров будет примерно равным, но В КАКОМ ПОРЯДКЕ И КАКИМИ СЕРИЯМИ будет выпадать та же «восьмёрка» на длинной дистанции – никто предсказать не может.

А теперь ответим на один важный вопрос:

Как правильно играть в азартные игры и лотереи? – в чём главный секрет?

Наверное, многие ожидают услышать от меня что-нибудь вроде: «Лучше вообще не играть», «Открыть собственное казино», «Организовать лотерею» и т.п. Ну почему же не играть? Игра – это одно из развлечений, а за развлечения, как известно, нужно… совершенно верно! Поэтому средства, на которые вы играете, следует считать платой за развлечение, но ни в коем случае трагической потерей. Что касается лотерей, то билет лучше покупать опять же ради развлечения и наобум. Или «по наитию». Правда, лично я никогда не слышал, чтобы кто-то из «счастливчиков» рассказывал о своём предчувствии.

Естественно, перечисленные советы не относятся к хроническим лудоманам и им как раз таки «Лучше вообще не играть». И после столь увлекательного отступления рассмотрим ещё несколько задач по теме:

Задача 70
Среди изделий, произведенных на станке-автомате, в среднем бывает 60% изделий первого сорта. Какова вероятность того, что среди 6 наудачу отобранных изделий будет:

а) от 2 до 4 изделий первого сорта;
б) не менее 5 изделий первого сорта;
в) хотя бы одно изделие более низкого сорта.

Вероятность производства первосортного изделия не зависит от качества других выпущенных изделий, поэтому в задаче речь идёт о независимых испытаниях. Пожалуйста, не подходите формально и не пренебрегайте подобным анализом условия, а то может статься, события-то зависимые или задача вообще о другом.

Решение: вероятность зашифрована под проценты, которые, напоминаю, нужно разделить на сто: – вероятность того, что выбранное изделие будет 1-го сорта. Тогда: – вероятность того, что оно не будет первосортным.

а) Событие «Среди 6 наудачу отобранных изделий будет от 2 до 4 изделий первого сорта» состоит в трёх несовместных исходах: среди изделий будет 2 первосортных или 3 первосортных, или 4 первосортных.

С исходами удобнее разделаться по отдельности. Трижды используем формулу Бернулли :

По теореме сложения вероятностей несовместных событий:
– вероятность того, что среди 6 наудачу отобранных изделий будет от 2 до 4 изделий первого сорта.

Решение можно было записать и «одной строкой», что мы и сделаем в следующем пункте:

б) Событие «Среди 6 наудачу отобранных изделий будет не менее 5 изделий первого сорта» состоит в двух несовместных исходах: первосортных изделий будет пять или шесть. По формуле Бернулли и теореме сложения вероятностей несовместных событий:

– искомая вероятность.

в) Вероятность того, что «Среди 6 наудачу отобранных изделий будет хотя бы одно изделие более низкого сорта» удобно найти через вероятность противоположного события («Все изделия будут первосортными»), которая уже известна:

– вероятность того, что среди шести отобранных изделий окажется хотя бы одно низкосортное.

Ответ: , и подобных задач пруд пруди.

Давайте заодно вспомним такое полезное понятие, как полная группа событий. Что осталось не найденным? Остались не найденными вероятности двух событий. Не хотел я лишний раз заострять внимание на Калькуляторе по теории вероятностей, который приложен к книге, но быстроты ради воспользуюсь:

– но на чистовике так, конечно, делать не нужно – обязательно расписывайте вычисления подробно!

Проверка:
,
что и требовалось проверить

Небольшое задание для самостоятельного решения:

Задача 71
Производится 8 выстрелов по цели, в каждом из которых вероятность попадания равна 0,1. Для разрушения цели требуется хотя бы два попадания. Найти вероятность того, что цель будет разрушена

Формула Бернулли очень удобна, но с другой стороны, обладает и рядом недостатков. В частности, при достаточно больших значениях и её применение затруднено ввиду огромных значений факториалов. В этом случае используют теоремы Лапласа. В другой распространённой на практике ситуации вероятность достаточно мала, а количество испытаний весьма велико. Здесь вопрос разрешается с помощью формулы Пуассона, с неё и начнём:

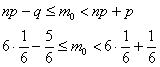
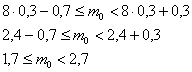
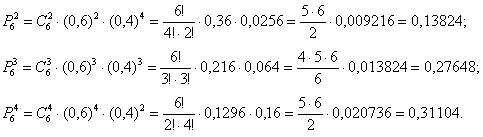
1.10. Формула Пуассона

1.8. Формулы Байеса

| Оглавление |

Полную и свежую версию этой книги в pdf-формате,
а также курсы по другим темам можно найти после Оглавления.

Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!

С наилучшими пожеланиями, Александр Емелин