|
Ваш репетитор, справочник и друг!
|
1.8. Формулы БайесаМатериал тесно связан с содержанием предыдущего параграфа. Пусть событие При условии, что событие На первый взгляд кажется полной нелепицей – зачем пересчитывать вероятности гипотез, если они и так известны? Но на самом деле разница есть:
Рассмотрим это различие на конкретном примере: Задача 60 Первая часть решения состоит в использовании формулы полной вероятности. Иными словами, вычисления проводятся в предположении, что испытание ещё не произведено и событие «изделие оказалось стандартным» пока не наступило. Рассмотрим две гипотезы: Всего: 4000 + 6000 = 10000 изделий на складе. По классическому определению: Контроль: Рассмотрим зависимое событие: В первой партии 100% – 20% = 80% стандартных изделий, поэтому: Аналогично, во второй партии 100% – 10% = 90% стандартных изделий и По формуле полной вероятности: Часть вторая. Пусть наудачу взятое со склада изделие оказалось стандартным. Эта фраза прямо прописана в условии, и она
констатирует тот факт, что событие а) б) После переоценки гипотезы Ответ: Понять смысл переоценки гипотез нам поможет Иван Васильевич, которой снова сменил профессию и стал директором завода. Он знает, что
сегодня 1-й цех отгрузил на склад 4000, а 2-й цех – 6000 изделий, и приходит удостовериться в этом. Предположим, вся продукция однотипна и
находится в одном контейнере. Естественно, Иван Васильевич подсчитал, что изделие, которое он сейчас извлечёт для проверки, с вероятностью
Но после того как выбранное изделие оказывается стандартным, он восклицает: «Какой же классный болт! – его скорее выпустил 2-й цех».
Таким образом, вероятность второй гипотезы переоценивается в лучшую сторону Вы скажете, чистый субъективизм? Отчасти – да, более того, сам Байес интерпретировал апостериорные вероятности как уровень доверия. И, несмотря на то, что у байесовского подхода немало критиков, в нём есть и объективное зерно. Ведь вероятности того, что изделие будет стандартным (0,8 и 0,9 для 1-го и 2-го цехов соответственно) это предварительные (априорные) и средние оценки. Но, выражаясь философски – всё течёт, всё меняется, и вероятности в том числе. Вполне возможно, что на момент
исследования более успешный 2-й цех повысил процент выпуска стандартных изделий (и / или 1-й цех снизил), и если
проверить бОльшее количество либо все 10 тысяч изделий на складе, то переоцененные значения Кстати, если Иван Васильевич извлечёт нестандартную деталь, то наоборот – он будет больше «подозревать» первый цех и меньше – второй. Предлагаю убедиться в этом самостоятельно: Задача 61 Условие отличатся двумя буквами, которые я выделил жирным шрифтом. Задачу можно решить с «чистого листа», или воспользоваться
результатами предыдущих вычислений. В образце я провёл полное решение, но чтобы не возникло формальной накладки с предыдущей задачей,
событие «наудачу взятое со склада изделие будет нестандартным» обозначено через Байесовская схема переоценки вероятностей встречается повсеместно, причём её активно эксплуатируют и различного рода мошенники. Рассмотрим ставшее нарицательным АО на три буквы, которое привлекает вклады населения, якобы куда-то их инвестирует, исправно выплачивает 2% в день и т.д. Что происходит? Проходит день за днём, месяц за месяцем и всё новые и новые факты, донесённые путём рекламы и «сарафанным радио», только повышают уровень доверия к финансовой пирамиде (апостериорная байесовская переоценка в связи с произошедшими событиями!). То есть, в глазах вкладчиков происходит постоянное увеличение вероятности того, что «это серьёзная контора»; при этом вероятность противоположной гипотезы («это очередной лохотрон»), само собой, уменьшается и уменьшается. Дальнейшее, думаю, понятно. Примечательно, что заработанная репутация даёт организаторам время успешно скрыться от Ивана Васильевича, который остался не только без партии болтов, но и без штанов. К не менее любопытным примерам мы вернёмся чуть позже, а пока на очереди, пожалуй, самый распространенный случай с тремя гипотезами: Задача 62 Заметьте, что в задачах на формулы Байеса в условии обязательно фигурирует некое произошедшее событие, в данном случае – покупка лампы. Событий прибавилось, и решение удобнее оформить в «быстром» стиле. Алгоритм точно такой же: на первом шаге находим вероятность того, что купленная лампа вообще окажется бракованной. Пользуясь исходными данными, переводим проценты в вероятности: Контроль: По формуле полной вероятности: Шаг второй. Пусть купленная лампа оказалась бракованной (событие произошло) По формуле Байеса: Ответ: Почему изначальная вероятность 2-й гипотезы Интересно заметить, что вероятности 1-й и 3-й гипотез, переоценились в ожидаемых направлениях и сравнялись: Контроль: К слову, о заниженных и завышенных оценках: Задача 63 а) он был подготовлен очень хорошо; Проведите вычисления и проанализируйте результаты переоценки гипотез. Что и говорить, репутация – это важнейший капитал, не случайно многие корпорации носят имена-фамилии своих отцов-основателей, которые руководили делом 100-200 лет назад и прославились своей безупречной репутацией. Да, байесовский подход в известной степени субъективен, но… так устроена жизнь! Закрепим материал заключительным индустриальным примером, в котором я расскажу ещё об одном техническом приёме решения: Решение: в отличие от предыдущих задач здесь в явном виде задан вопрос, который разрешается с помощью формулы полной вероятности. Но с другой стороны, условие немного «зашифровано», и разгадать этот ребус нам поможет школьный навык составлять простейшие уравнения. За «икс» удобно принять наименьшее значение: Пусть По условию, первый цех производит в 4 раза больше третьего цеха, поэтому доля 1-го цеха составляет Составим и решим уравнение: Таким образом: Контроль: За «икс» изначально можно было принять долю 1-го либо долю 2-го цеха – вероятности выйдёт такими же. Но, так или иначе, самый трудный участок пройден, и решение входит в накатанную колею: Из условия находим: По формуле полной вероятности: Вопрос второй: какова вероятность Коль скоро в условии нет пунктов «а» и «бэ», то ответ лучше снабдить текстовыми комментариями: Ответ: Как видите, задачи на формулу полной вероятности и формулы Байеса достаточно простЫ, и, наверное, по этой причине в них так часто пытаются затруднить условие, о чём я уже упоминал в начале параграфа.
|
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Практикум по теории вероятностей
Практикум по теории вероятностей Научись решать в считанные дни!
Научись решать в считанные дни!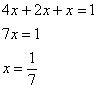
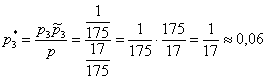 – искомая вероятность. Совершенно
ожидаемо – ведь третий цех производит не только самую малую долю деталей, но и лидирует по качеству!
– искомая вероятность. Совершенно
ожидаемо – ведь третий цех производит не только самую малую долю деталей, но и лидирует по качеству! 1.9. Независимые испытания и формула Бернулли
1.9. Независимые испытания и формула Бернулли  1.7. Формула полной вероятности
1.7. Формула полной вероятности