Ваш репетитор, справочник и друг!

Практикум по теории вероятностей

Научись решать в считанные дни!

1.7. Формула полной вероятности

Это непосредственное следствие только что разобранных теорем, и даже задача такая была недавно (Задача 54).

Рассмотрим зависимое событие , которое может произойти лишь в результате осуществления одной из несовместных гипотез , которые образуют полную группу. Пусть известны вероятности этих гипотез и соответствующие условные вероятности .
Тогда вероятность наступления события равна:

Эта формула получила название формулы полной вероятности. В учебниках она формулируется теоремой, доказательство которой элементарно: согласно алгебре событий, событие расписывается в виде суммы , которая обозначает, что:

– произошло событие и после него наступило событие или произошло событие и после него наступило событие , или произошло событие и после него наступило событие , или …., или произошло событие и после него наступило событие .

Поскольку гипотезы несовместны, а событие – зависимо, то по теореме сложения вероятностей несовместных событий (первый шаг) и теореме умножения вероятностей зависимых событий (второй шаг), получаем:

И, наверное, многие предчувствуют содержание первого примера :)

Куда ни плюнь – везде урна:

Задача 56
Имеются три одинаковые урны. В первой урне находятся 4 белых и 7 черных шаров, во второй – только белые и в третьей – только черные шары. Наудачу выбирается одна урна и из неё наугад извлекается шар. Какова вероятность того, что этот шар чёрный?

Решение: рассмотрим событие – из наугад выбранной урны будет извлечён чёрный шар. Данное событие может произойти или не произойти в результате осуществления одной из следующих гипотез:
– будет выбрана 1-я урна;
– будет выбрана 2-я урна;
– будет выбрана 3-я урна.

Так как урна выбирается наугад, то выбор любой из трёх урн равновозможен, следовательно:

Перечисленные гипотезы образуют полную группу событий, то есть, по условию, шар может появиться только из этих урн, а например, не прилететь с бильярдного стола. Проведём простую промежуточную проверку:
, ОК, едем дальше:

В первой урне 4 белых + 7 черных = 11 шаров, по классическому определению:
– вероятность извлечения чёрного шара при условии, что будет выбрана 1-я урна.

Во второй урне только белые шары, поэтому в случае её выбора появление чёрного шара становится невозможным:
.

И, наконец, в третьей урне одни чёрные шары, а значит, соответствующая условная вероятность извлечения чёрного шара составит (событие достоверно).

По формуле полной вероятности:

– вероятность того, что из наугад выбранной урны будет извлечен чёрный шар.

Ответ:

Разобранный пример снова наводит на мысль о том,
как важно ВНИКАТЬ В УСЛОВИЕ.

Возьмём те же задачи с урнами и шарами – при их «внешней схожести» способы решения могут быть совершенно разными: где-то требуется применить только классическое определение вероятности, где-то события независимы, где-то зависимы, а где-то речь о гипотезах. При этом не существует чёткого формального критерия для выбора пути решения – над ним почти всегда нужно думать.

Как повысить свою квалификацию? Решаем, решаем и ещё раз решаем!

Задача 57
В тире имеются 5 различных по точности боя винтовок. Вероятности попадания в мишень для данного стрелка соответственно равны и 0,4. Чему равна вероятность попадания в мишень, если стрелок делает один выстрел из случайно выбранной винтовки?

Краткое решение и ответ в конце книги.

В большинстве тематических задач гипотезы, конечно же, не равновероятны:

Задача 58
В пирамиде 5 винтовок, три из которых снабжены оптическим прицелом. Вероятность того, что стрелок поразит мишень при выстреле из винтовки с оптическим прицелом, равна 0,95; для винтовки без оптического прицела эта вероятность равна 0,7. Найти вероятность того, что мишень будет поражена, если стрелок производит один выстрел и наудачу взятой винтовки.

Решение: в этой задаче количество винтовок точно такое же, как и в предыдущей, но вот гипотезы всего две:
– стрелок выберет винтовку с оптическим прицелом;
– стрелок выберет винтовку без оптического прицела.

По классическому определению вероятности:
.

Контроль:

Рассмотрим событие: – стрелок поразит мишень из наугад взятой винтовки.
По условию: .

По формуле полной вероятности:

Ответ: 0,85

На практике решение удобно оформить коротко, примерно так:

Решение: по классическому определению: – вероятности выбора винтовки с оптическим и без оптического прицела соответственно.
По условию, – вероятности попадания в мишень из соответствующих типов винтовок.
По формуле полной вероятности:
– вероятность того, что стрелок поразит мишень из наугад выбранной винтовки.

Ответ: 0,85

Следующая задача для самостоятельного решения:

Задача 59
Двигатель работает в трёх режимах: нормальном, форсированном и на холостом ходу. В режиме холостого хода вероятность его выхода из строя равна 0,05, при нормальном режиме работы – 0,1, а при форсированном – 0,7. 70% времени двигатель работает в нормальном режиме, а 20% – в форсированном. Какова вероятность выхода из строя двигателя во время работы?

На всякий случай напомню – чтобы получить значения вероятностей проценты нужно разделить на 100. Будьте очень внимательны! По моим наблюдениям, условия задач на формулу полной вероятности частенько пытаются подзапутать, и я специально подобрал такой пример. Скажу по секрету, сам чуть не запутался :)

Образец решения оформлен коротким способом.

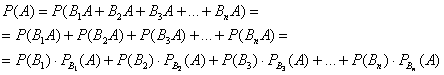
1.8. Формулы Байеса

1.6.6. Теорема умножения вероятностей зависимых событий

| Оглавление |

Полную и свежую версию этой книги в pdf-формате,
а также курсы по другим темам можно найти после Оглавления.

Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!

С наилучшими пожеланиями, Александр Емелин